题目内容
若函数y=
是奇函数,当x>0时,其对应的图象如图所示,则f(x)等于 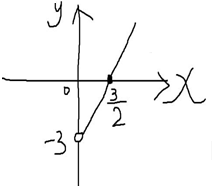
|

考点:函数奇偶性的性质
专题:函数的性质及应用
分析:首先根据函数的图象求出函数g(x)的解析式,进一步利用函数是奇函数求出函数f(x)的解析式.
解答:
解:如图所示:设函数g(x)的解析式为g(x)=kx+b,函数图象经过(0,-3)和(
,0)
则解得:g(x)=2x-3
由于y=
是奇函数.
则:f(x)=-g(-x)=2x+3
故答案为:f(x)=2x+3(x<0)
| 3 |
| 2 |
则解得:g(x)=2x-3
由于y=
|
则:f(x)=-g(-x)=2x+3
故答案为:f(x)=2x+3(x<0)
点评:本题考查的知识要点:函数解析式的确定,奇函数性质的应用,属于基础题型.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
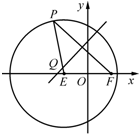 如图,已知圆E:
如图,已知圆E: