Question

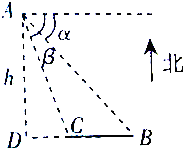如图，从气球A测得正前方的济南全运会东荷、西柳两个场馆B、C的俯角分别为α、β，此时气球的高度为h，则两个场馆B、C间的距离为（　　）

• A、

  hsinαsinβ

  sin(α-β)

• B、

  hsin(β-α)

  sinαsinβ

• C、

  hsinα

  sinβsin(α-β)

• D、

  hsinβ

  sinαsin(α-β)

Answer 1

考点：解三角形的实际应用

专题：计算题,解三角形

分析：过A作垂线AD交CB于D，由题意可得∠ABD=α，AB=

h

sinα

，∠ACB=π-β，∠BAC=β-α，在△ABC中利用正弦定理，可求BC

解答： 解：过A作垂线AD交CB于D，则在Rt△ADB中，∠ABD=α，AB=

h

sinα

．                       
又在△ACB中，∠ACB=π-β，∠BAC=β-α，
由正弦定理，得BC=

hsin(β-α)

sinsinβ

即两个场馆B、C间的距离为

hsin(β-α)

sinsinβ

．
故选：B．

点评：本题主要考查了正弦定理在解决实际问题中的应用，解决本题的关键是要把实际问题转化为数学问题，还要知道俯角的概念．