题目内容
设函数f(x)=
(1)画出函数y=f(x)的图象.
(2)讨论方程|f(x)|=a的解的个数.(只写明结果,无需过程)
|
(1)画出函数y=f(x)的图象.
(2)讨论方程|f(x)|=a的解的个数.(只写明结果,无需过程)
考点:分段函数的应用,函数的图象
专题:函数的性质及应用
分析:本题(1)分段画出函数数y=f(x)的图象,一段是直线的一部分,另一段是抛物线的一部分;(2)利用(1)的图象,画出函数y=|f(x)|的图象,再利用直线y=a与曲线y=|f(x)|的交点情况,得到方程|f(x)|=a的解的个数.
解答:
(1)函数y=f(x)的图象如图.
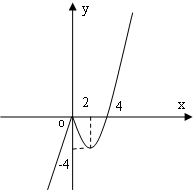
(2)函数y=|f(x)|的图象如图.
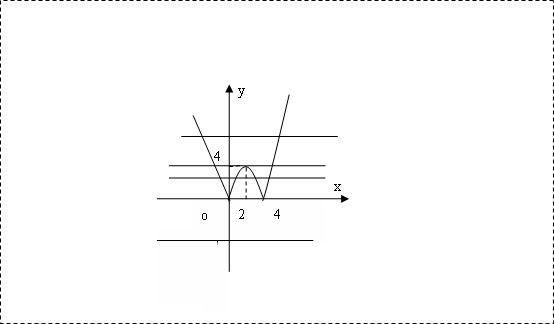
①0<a<4时,方程有四个解;
②a=4时,方程有三个解;
③a=0或a>4时,方程有二个解;
④a<0时,方程没有实数解.

(2)函数y=|f(x)|的图象如图.

①0<a<4时,方程有四个解;
②a=4时,方程有三个解;
③a=0或a>4时,方程有二个解;
④a<0时,方程没有实数解.
点评:本题考查了分段函数的图象、绝对值函数的图象,还考查了分类讨论的数学思想,本题有一定的思维难度,属于中档题.

练习册系列答案
相关题目
设{an}为等差数列,|a3|=|a9|,公差d<0,则使前n项和Sn取得最大值时正整数n=( )
| A、4或5 | B、5或6 |
| C、6或7 | D、8或9 |
已知f(x)=x2+bx+c,且f(1)=f(3)=0,则f(x)的单调递减区间为( )
| A、(-∞,1)或(3 ,+∞) |
| B、(1,3) |
| C、(-∞,2) |
| D、(2,+∞) |
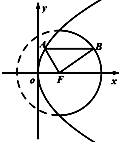 已知△ABF,点F(2,0),点A,B分别在图中抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△ABF的周长的取值范围是
已知△ABF,点F(2,0),点A,B分别在图中抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△ABF的周长的取值范围是