题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c,已知c=2,C=
.
(1)若△ABC的面积等于
,求a,b;
(2)若cosA=
,求b.
| π |
| 3 |
(1)若△ABC的面积等于
| 3 |
(2)若cosA=
| ||
| 3 |
考点:余弦定理
专题:解三角形
分析:(1)由三角形的面积公式表示出三角形ABC的面积,将sinC的值代入求出ab的值,再由余弦定理列出关系式,利用完全平方公式变形后,将ab的值代入即可求出a+b的值,由此求得a、b的值.
(2)由cosA=
,求得 sinA=
,由正弦定理求得a的值.再求得sinB=sin(A+C) 的值,由
=
,求得b的值.
(2)由cosA=
| ||
| 3 |
| ||
| 3 |
| b |
| sinB |
| c |
| sinC |
解答:
解:(1)∵S△ABC=
absinC=
ab=
,∴ab=4①.
由余弦定理c2=a2+b2-2abcosC=a2+b2-ab=(a+b)2-3ab,即4=(a+b)2-12,则a+b=4 ②.
由①②求得 a=b=2.
(2)∵cosA=
,∴sinA=
,由正弦定理可得
=
,即
=
,求得a=
.
又sinB=sin(A+C)=sinAcosC+cosAsinC=
×
+
×
=
,
故由
=
,即
=
,求得b=
.
| 1 |
| 2 |
| ||
| 4 |
| 3 |
由余弦定理c2=a2+b2-2abcosC=a2+b2-ab=(a+b)2-3ab,即4=(a+b)2-12,则a+b=4 ②.
由①②求得 a=b=2.
(2)∵cosA=
| ||
| 3 |
| ||
| 3 |
| a |
| sinA |
| c |
| sinC |
| a | ||||
|
| 2 | ||||
|
4
| ||
| 3 |
又sinB=sin(A+C)=sinAcosC+cosAsinC=
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 2 |
3+
| ||
| 6 |
故由
| b |
| sinB |
| c |
| sinC |
| b | ||||
|
| 2 | ||||
|
2(
| ||||
| 3 |
点评:此题考查了正弦定理、余弦定理的应用,三角形的面积公式,以及完全平方公式的运用,属于基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
下列给出的赋值语句中正确的是( )
| A、4=M | B、M=-M |
| C、B=A-3 | D、x+y=0 |
已知等差数列{an}的前n项和Sn,满足Sn=-
n2+2n,则Sn的最大值为( )
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
若奇函数f(x)在区间[3,7]上是减函数且有最大值4,则f(x)在区间[-7,-3]上是( )
| A、增函数且最小值为-4 |
| B、增函数且最大值为-4 |
| C、减函数且最小值为-4 |
| D、减函数且最大值为-4 |
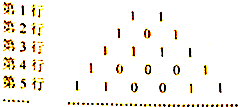 将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是
将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是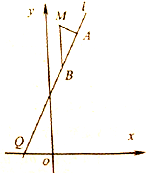 如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=
如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=