题目内容
设{an}为等差数列，|a3|=|a9|，公差d＜0，则使前n项和Sn取得最大值时正整数n=（ ）
| A、4或5 | B、5或6 |
| C、6或7 | D、8或9 |
考点：等差数列的前n项和,数列的函数特性
专题：等差数列与等比数列
分析：由已知中等差数列{an}中，|a3|=|a9|，公差d＜0，构造方程我们易求出数列{an}的首项为a1与公差为d的关系，进而得到数列{an}中正项与负项的分界点，进而得到使前n项和取最大值的正整数n．
解答：
解：设等差数列{an}的首项为a1，公差为d，
∵|a3|=|a9|，
∴|a1+2d|=|a1+8d|
解得a1=-5d或d=0（舍去）
则a1+5d=a6=0
a5＞0
故使前n项和取最大值的正整数n是5或6．
故选：B．
∵|a3|=|a9|，
∴|a1+2d|=|a1+8d|
解得a1=-5d或d=0（舍去）
则a1+5d=a6=0
a5＞0
故使前n项和取最大值的正整数n是5或6．
故选：B．
点评：本题考查的知识点是等差数列的定义及等差数列的性质，在处理等差数列问题时，常设出数列{an}的首项为a1，公差为d，然后构造方程分析首项为a1与公差为d的关系．
练习册系列答案
相关题目
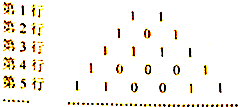将二项式系数表中的奇数换成1，偶数换成0，得到如图所示的0-1三角数表，从上往下数，第1次全行的数都为1的是第1行，第二次全行的数都为1的是第3行，…，那么第61行中1的个数是命题p：x（x-3）=0，命题q：x=3，则命题p是命题q的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |