题目内容
定义在实数集R函数f（x）满足f（x）+f（x+2）=0，且f（x-1）为奇函数，现有以下三种叙述：
（1）8是函数f（x）的一个周期；
（2）f（x）的图象关于点（3，0）对称；
（3）f（x）是偶函数．
其中正确的是（ ）
（1）8是函数f（x）的一个周期；
（2）f（x）的图象关于点（3，0）对称；
（3）f（x）是偶函数．
其中正确的是（ ）
| A、（2）（3） |
| B、（1）（2） |
| C、（1）（3） |
| D、（1）（2）（3） |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：首先，根据f（x）+f（x+2）=0，得到f（x+4）=f（x），函数f（x）的一个周期为4，然后，结合f（x-1）为奇函数，进一步判断即可．
解答：
解：对于（1）：∵f（x）+f（x+2）=0，
∴f（x+2）=-f（x），
∴f（x+4）=f（x），
∴函数f（x）的一个周期为4，
∴8是函数f（x）的一个周期，
故（1）正确；
对于（2）：∵f（x-1）为奇函数，并结合（1）得：
函数f（x）的图象关于点（3，0）对称，
故（2）正确；
对于（3）：结合（1），（2）得（3）正确；
故选：D．
∴f（x+2）=-f（x），
∴f（x+4）=f（x），
∴函数f（x）的一个周期为4，
∴8是函数f（x）的一个周期，
故（1）正确；
对于（2）：∵f（x-1）为奇函数，并结合（1）得：
函数f（x）的图象关于点（3，0）对称，
故（2）正确；
对于（3）：结合（1），（2）得（3）正确；
故选：D．
点评：本题重点考查了奇函数的性质、周期性、对称性等知识，属于中档题．
练习册系列答案
相关题目
一个几何体的三视图如图所示，则该几何体的表面积为（ ）
A、
| ||||
B、9+4
| ||||
C、9+3
| ||||
D、
|
设f（x）是周期为4的奇函数，当0≤x≤2时，f（x）=x（2-x），则f（-5）等于（ ）
| A、1 | B、-1 | C、3 | D、-3 |
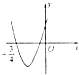如图是函数f（x）=x2-ax+b的大致图象，则函数g（x）=log2x+f′（x）的零点所在的区间是（ ）A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
函数f（x）=ax2-ax+1（a≠0），如果f（-k）＜0，则f（k+1）的值是（ ）
| A、正数 | B、负数 | C、零 | D、无法确定 |
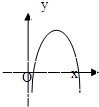
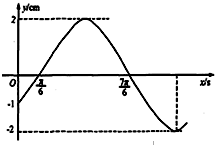如图是某简谐运动的一段图象，其函数模型是f（x）=Asin（ωx+φ）（x≥0），其中A＞0，ω＞0，-