题目内容
定义域在R上奇函数f(x)满足f(x+
)=-f(x),f(1)>-1,f(4)=loga2(a>0且a≠1),则实数a的取值范围是 .
| 5 |
| 2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:首先,根据f(x+
)=-f(x),得到f(x)是周期为5的函数,然后,得到f(1)=-loga2,再结合f(1)>-1,得到loga2<1=logaa,对a的取值进行分类讨论,得到答案.
| 5 |
| 2 |
解答:
解:∵f(x+
)=-f(x),
∴f(x+5)=f(x),
∴f(x)是周期为5的函数,
∵f(4)=f(5-1)=f(-1)=-f(1)=loga2
∴f(1)=-loga2
又∵f(1)>-1,
∴-loga2>-1,
∴loga2<1=logaa,
∴当0<a<1时,
∴a<2,
∴此时,0<a<1
当a>1时,
∴a>2,
此时,0<a<1
综上,a>2或0<a<1
故答案为:(0,1)∪(2,+∞)
| 5 |
| 2 |
∴f(x+5)=f(x),
∴f(x)是周期为5的函数,
∵f(4)=f(5-1)=f(-1)=-f(1)=loga2
∴f(1)=-loga2
又∵f(1)>-1,
∴-loga2>-1,
∴loga2<1=logaa,
∴当0<a<1时,
∴a<2,
∴此时,0<a<1
当a>1时,
∴a>2,
此时,0<a<1
综上,a>2或0<a<1
故答案为:(0,1)∪(2,+∞)
点评:本题综合考查了奇函数的性质、周期函数、对数函数的单调性等知识,属于中档题.注意分类讨论思想在解题中的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若
=a+bi,(a,b∈R),则(a,b)为( )
| 1 |
| 1-i |
A、(
| ||||
B、(-
| ||||
| C、(1,1) | ||||
| D、(1,-1) |
定义在R上的奇函数f(x)满足f(2-x)=f(x),且在[-3,-2]上是减函数,α,β是钝角三角形的两个锐角,则f(sinα)与f(cosβ)的大小关系是( )
| A、f(sinα)>f(cosβ) |
| B、f(sinα)<f(cosβ) |
| C、f(sinα)=f(cosβ) |
| D、f(sinα)≥f(cosβ) |
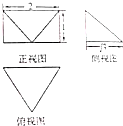
一个几何体的三视图如图所示,则该几何体的表面积为( )


A、
| ||||
B、9+4
| ||||
C、9+3
| ||||
D、
|
设f(x)是周期为4的奇函数,当0≤x≤2时,f(x)=x(2-x),则f(-5)等于( )
| A、1 | B、-1 | C、3 | D、-3 |
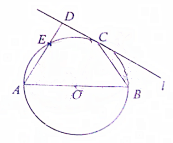 如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长为
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长为