题目内容
已知集合A={1，3，m}，B={1，
}，A∩B=B，那么m=（ ）
| m |
A、0或
| ||
| B、0或9 | ||
C、1或
| ||
| D、1或9 |
考点：交集及其运算
专题：集合
分析：根据A，B，且A与B的交集为B，确定出m的值即可．
解答：
解：∵A={1，3，m}，B={1，
}，且A∩B=B，
∴
=3或
=m，
解得：m=9或m=1或m=0，
当m=9时，A={1，3，9}，B={1，3}，满足A∩B=B；
当m=1时，A中有2个元素，B中有一个元素，不合题意，舍去；
当m=0时，A={0，1，3}，B={0，1}，满足A∩B=B，
综上，m=0或9．
故选：B．
| m |
∴
| m |
| m |
解得：m=9或m=1或m=0，
当m=9时，A={1，3，9}，B={1，3}，满足A∩B=B；
当m=1时，A中有2个元素，B中有一个元素，不合题意，舍去；
当m=0时，A={0，1，3}，B={0，1}，满足A∩B=B，
综上，m=0或9．
故选：B．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
定义在R上的奇函数f（x）满足f（2-x）=f（x），且在[-3，-2]上是减函数，α，β是钝角三角形的两个锐角，则f（sinα）与f（cosβ）的大小关系是（ ）
| A、f（sinα）＞f（cosβ） |
| B、f（sinα）＜f（cosβ） |
| C、f（sinα）=f（cosβ） |
| D、f（sinα）≥f（cosβ） |
已知函数f（x）=|log2x|-m（m＞0）的零点分别为x1，x2（x1＜x2），函数g（x）=|log2x|-
（m＞0）的零点分别为x3，x4（x3＜x4），则
的最小值为（ ）
| 8 |
| 2m+1 |
| |x2-x4| |
| |x1-x3| |
A、4
| |||
B、8
| |||
C、4
| |||
D、8
|
设f（x）是周期为4的奇函数，当0≤x≤2时，f（x）=x（2-x），则f（-5）等于（ ）
| A、1 | B、-1 | C、3 | D、-3 |
设Sn为等差数列{an}的前n项和，若a1=1，公差d=2，Sn+2-Sn=36，则n=（ ）
| A、5 | B、6 | C、7 | D、8 |
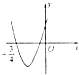如图是函数f（x）=x2-ax+b的大致图象，则函数g（x）=log2x+f′（x）的零点所在的区间是（ ）A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
