题目内容
 已知抛物线C:x2=2py(p>0),直线l:y=x+1与抛物线C交于A,B两点,设直线OA,OB的斜率分别为k1.k2(其中O为坐标原点),且k1•k2=-
已知抛物线C:x2=2py(p>0),直线l:y=x+1与抛物线C交于A,B两点,设直线OA,OB的斜率分别为k1.k2(其中O为坐标原点),且k1•k2=-| 1 |
| 4 |
(1)求p的值;
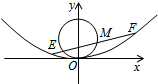
(2)如图,已知点M(x0,y0)为圆:x2+y2-y=0上异于O点的动点,过点M的直线m交抛物线C于E,F两点.若M为线段EF的中点,求|EF|的最大值.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)直线l:y=x+1,代入抛物线方程,利用韦达定理,结合k1•k2=-
,求p的值;
(2)直线m:y=k(x-x0)+y0,代入x2=4y可得x2-4kx+4kx0-4y0=0,求出|EF|,利用基本不等式,即可求|EF|的最大值.
| 1 |
| 4 |
(2)直线m:y=k(x-x0)+y0,代入x2=4y可得x2-4kx+4kx0-4y0=0,求出|EF|,利用基本不等式,即可求|EF|的最大值.
解答:
解:(1)设A(x1,y1),B(x2,y2),
直线l:y=x+1,代入抛物线方程可化为x2-2px-2p=0,∴x1x2=-2p,
∴k1•k2=
=-
=-
,
∴p=2;
(2)设E(x3,y3),F(x4,y4),直线m:y=k(x-x0)+y0,
代入x2=4y可得x2-4kx+4kx0-4y0=0,
∴x3+x4=4k=2x0,
∴k=
x0,
∴x2-2x0x+2x02-4y0=0,
△=16y0-4x02,
∴|EF|=
|x3-x4|=
,
∵x02+y02-y0=0,
∴|EF|=
≤
=2+2y0≤4,
当且仅当y0=1时,|EF|的最大值为4.
直线l:y=x+1,代入抛物线方程可化为x2-2px-2p=0,∴x1x2=-2p,
∴k1•k2=
| x1x2 |
| 4p2 |
| 1 |
| 2p |
| 1 |
| 4 |
∴p=2;
(2)设E(x3,y3),F(x4,y4),直线m:y=k(x-x0)+y0,
代入x2=4y可得x2-4kx+4kx0-4y0=0,
∴x3+x4=4k=2x0,
∴k=
| 1 |
| 2 |
∴x2-2x0x+2x02-4y0=0,
△=16y0-4x02,
∴|EF|=
| 1+k2 |
| (4+x02)(4y0-x02) |
∵x02+y02-y0=0,
∴|EF|=
| (4+y0-y02)(3y0+y02) |
| (4+y0-y02)+(3y0+y02) |
| 2 |
当且仅当y0=1时,|EF|的最大值为4.
点评:本题考查抛物线方程,考查直线与抛物线的位置关系,考查基本不等式的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在正方体8个顶点中任选3个顶点连成三角形,则所得的三角形是等腰直角三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|