题目内容
在正方体8个顶点中任选3个顶点连成三角形,则所得的三角形是等腰直角三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:总的事件数是C83,而从正方体的8个顶点中任取3个顶点可形成的等腰直角三角形的个数按所选取的三个顶点是只能是来自于该正方体的同一个面.根据概率公式计算即可.
解答:
解:正方体8个顶点中任选3个顶点连成三角形,所得的三角形是等腰直角三角形只能在各个面上,在每一个面上能组成等腰直角三角形的有四个,
所以共有4×6=24个,
而在8个点中选3个点的有C83=56,
所以所求概率为
=
故选:C
所以共有4×6=24个,
而在8个点中选3个点的有C83=56,
所以所求概率为
| 24 |
| 56 |
| 3 |
| 7 |
故选:C
点评:本题是一个古典概型问题,学好古典概型可以为其它概率的学习奠定基础,同时有利于理解概率的概念,有利于计算一些事件的概率,有利于解释生活中的一些问题.

练习册系列答案
相关题目
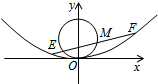 已知抛物线C:x2=2py(p>0),直线l:y=x+1与抛物线C交于A,B两点,设直线OA,OB的斜率分别为k1.k2(其中O为坐标原点),且k1•k2=-
已知抛物线C:x2=2py(p>0),直线l:y=x+1与抛物线C交于A,B两点,设直线OA,OB的斜率分别为k1.k2(其中O为坐标原点),且k1•k2=-


