题目内容
已知向量
=(1,1),
=(2,n),若|
+
|=|
-
|,则n= .
| a |
| b |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:运用向量的平方即为模的平方的性质,可得
•
=0,再由向量的或塑料件的坐标表示,计算即可得到.
| a |
| b |
解答:
解:若|
+
|=|
-
|,
则(
+
)2=(
-
)2,
即有
2+
2+2
•
=
2+
2-2
•
,
即为
•
=0,
由向量
=(1,1),
=(2,n),
则2+n=0,
解得n=-2.
故答案为:-2.
| a |
| b |
| a |
| b |
则(
| a |
| b |
| a |
| b |
即有
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
即为
| a |
| b |
由向量
| a |
| b |
则2+n=0,
解得n=-2.
故答案为:-2.
点评:本题考查向量的数量积的坐标表示和性质,主要考查向量的平方即为模的平方,属于基础题.

练习册系列答案
相关题目
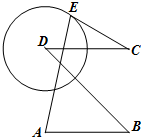 如图所示,正方形ABCD边长为2,圆D的半径为1,E是圆D上任意一点,则
如图所示,正方形ABCD边长为2,圆D的半径为1,E是圆D上任意一点,则| AE |
| CE |
A、1+2
| ||
B、-1-2
| ||
C、1-
| ||
D、1-2
|
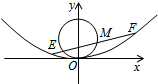 已知抛物线C:x2=2py(p>0),直线l:y=x+1与抛物线C交于A,B两点,设直线OA,OB的斜率分别为k1.k2(其中O为坐标原点),且k1•k2=-
已知抛物线C:x2=2py(p>0),直线l:y=x+1与抛物线C交于A,B两点,设直线OA,OB的斜率分别为k1.k2(其中O为坐标原点),且k1•k2=- 设非零向量向量
设非零向量向量 已知:如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E,连接EA交⊙O于点F.求证:
已知:如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E,连接EA交⊙O于点F.求证: