题目内容
已知函数f(x)=(1-tan
)[1+
sin(x+
)].
(1)求f(
)的值;
(2)若2sinα+f(α)=
,求
的值.
| x |
| 2 |
| 2 |
| π |
| 4 |
(1)求f(
| π |
| 6 |
(2)若2sinα+f(α)=
| 4 |
| 3 |
| ||||
| 1+tanα |
考点:三角函数中的恒等变换应用,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=2cosx,从而可求f(
)的值.
(2)由(1)及2sinα+f(α)=
可得sinα+cosα=
,两边平方可解得:sin2α=-
,从而化简
=
=sin2α,即可得解.
| π |
| 6 |
(2)由(1)及2sinα+f(α)=
| 4 |
| 3 |
| 2 |
| 3 |
| 5 |
| 9 |
| ||||
| 1+tanα |
| sin2α-cos2α+1 |
| 1+tanα |
解答:
解:(1)∵f(x)=(1-tan
)[1+
sin(x+
)]=(1-tan
)(1+sinx+cosx)=2cosx,
∴f(
)=2cos(
)=
.
(2)∵2sinα+f(α)=
,即有:2sinα+2cosα=
,
∴sinα+cosα=
,
∴两边平方可得:1+sin2α=
,可解得:sin2α=-
,
∴
=
=sin2α=-
.
| x |
| 2 |
| 2 |
| π |
| 4 |
| x |
| 2 |
∴f(
| π |
| 6 |
| π |
| 6 |
| 3 |
(2)∵2sinα+f(α)=
| 4 |
| 3 |
| 4 |
| 3 |
∴sinα+cosα=
| 2 |
| 3 |
∴两边平方可得:1+sin2α=
| 4 |
| 9 |
| 5 |
| 9 |
∴
| ||||
| 1+tanα |
| sin2α-cos2α+1 |
| 1+tanα |
| 5 |
| 9 |
点评:本题主要考查了三角函数中的恒等变换应用,同角三角函数基本关系的运用,考查了万能公式的应用,属于基本知识的考查.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
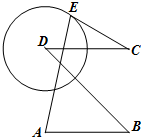 如图所示,正方形ABCD边长为2,圆D的半径为1,E是圆D上任意一点,则
如图所示,正方形ABCD边长为2,圆D的半径为1,E是圆D上任意一点,则| AE |
| CE |
A、1+2
| ||
B、-1-2
| ||
C、1-
| ||
D、1-2
|
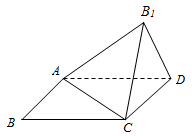 已知四边形ABCD是矩形,BC=kAB(k∈R),将△ABC沿着对角线AC翻折,得到△AB1C,设顶点B1在平面ABCD上的投影为O.
已知四边形ABCD是矩形,BC=kAB(k∈R),将△ABC沿着对角线AC翻折,得到△AB1C,设顶点B1在平面ABCD上的投影为O. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.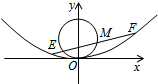 已知抛物线C:x2=2py(p>0),直线l:y=x+1与抛物线C交于A,B两点,设直线OA,OB的斜率分别为k1.k2(其中O为坐标原点),且k1•k2=-
已知抛物线C:x2=2py(p>0),直线l:y=x+1与抛物线C交于A,B两点,设直线OA,OB的斜率分别为k1.k2(其中O为坐标原点),且k1•k2=-