题目内容
设3,4,x是一个钝角三角形的三边长,且x是最大边,则x的取值范围是 .
考点:余弦定理
专题:解三角形
分析:由题意和余弦定理列出不等式,求出x的范围,由三边关系求出x的取值范围,再把它们并在一起.
解答:
解:因为x是一个钝角三角形的最大边,
所以x所对的角一定是钝角,
由余弦定理得,
<0,解得x>5,
又
,则1<x<7,
综上可得,5<x<7,x的取值范围是(5,7),
故答案为:(5,7).
所以x所对的角一定是钝角,
由余弦定理得,
| 32+42-x2 |
| 2×3×4 |
又
|
综上可得,5<x<7,x的取值范围是(5,7),
故答案为:(5,7).
点评:本题考查余弦定理,边角关系,以及三角形中的三边关系,容易忽略三角形中的三边关系.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
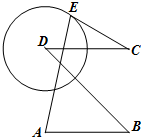 如图所示,正方形ABCD边长为2,圆D的半径为1,E是圆D上任意一点,则
如图所示,正方形ABCD边长为2,圆D的半径为1,E是圆D上任意一点,则| AE |
| CE |
A、1+2
| ||
B、-1-2
| ||
C、1-
| ||
D、1-2
|
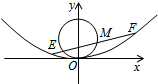 已知抛物线C:x2=2py(p>0),直线l:y=x+1与抛物线C交于A,B两点,设直线OA,OB的斜率分别为k1.k2(其中O为坐标原点),且k1•k2=-
已知抛物线C:x2=2py(p>0),直线l:y=x+1与抛物线C交于A,B两点,设直线OA,OB的斜率分别为k1.k2(其中O为坐标原点),且k1•k2=- 如图所示,在等腰直角三角形ABC中,AC=AB=2
如图所示,在等腰直角三角形ABC中,AC=AB=2



 设非零向量向量
设非零向量向量