题目内容
若命题“?x∈R，使x2+ax+1＜0”的否定是假命题，则实数a的取值范围是 ．
考点：命题的真假判断与应用,命题的否定
专题：简易逻辑
分析：由命题“?x∈R，使x2+ax+1＜0”的否定是假命题，可得命题“?x∈R，使x2+ax+1＜0”是真命题，因此△＞0，解出即可．
解答：
解：∵命题“?x∈R，使x2+ax+1＜0”的否定是假命题，
∴命题“?x∈R，使x2+ax+1＜0”是真命题，
∴△=a2-4＞0，解得a＞2或a＜-2．
∴实数a的取值范围是a＞2或a＜-2．
故答案为：a＞2或a＜-2．
∴命题“?x∈R，使x2+ax+1＜0”是真命题，
∴△=a2-4＞0，解得a＞2或a＜-2．
∴实数a的取值范围是a＞2或a＜-2．
故答案为：a＞2或a＜-2．
点评：本题考查了简易逻辑的判定、一元二次不等式的解集与判别式的关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
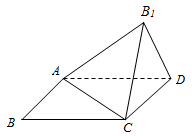已知四边形ABCD是矩形，BC=kAB（k∈R），将△ABC沿着对角线AC翻折，得到△AB1C，设顶点B1在平面ABCD上的投影为O．设集合M={y|y=|cos2x-sin2x|，x∈R}，N={x|y=ln（1-x2）}，则M∩N=（ ）
| A、{x|-1≤x≤1} |
| B、{x|-1≤x≤0} |
| C、{x|0＜x≤1} |
| D、{x|0≤x＜1} |
已知抛物线C：x2=2py（p＞0），直线l：y=x+1与抛物线C交于A，B两点，设直线OA，OB的斜率分别为k1．k2（其中O为坐标原点），且k1•k2=-