题目内容
15.如果曲线2|x|-y-4=0与曲线x2+λy2=4(λ<0)恰好有两个不同的公共点,则实数λ的取值范围是[-$\frac{1}{4}$,0).分析 去绝对值可得x≥0时,y=2x-4;当x<0时,y=-2x-4,数形结合可得曲线必相交于(±2,0),分别联立方程结合一元二次方程根的分布可得.
解答 解:由2|x|-y-4=0可得y=2|x|-4,
当x≥0时,y=2x-4;当x<0时,y=-2x-4,
∴函数y=2|x|-4的图象与方程x2+λy2=4的曲线必相交于(±2,0)
∴为了使函数y=2|x|-4的图象与方程x2+λy2=1的曲线恰好有两个不同的公共点,
则y=2x-4代入方程x2+λy2=1,整理可得(1+4λ)x2-16λx+16λ-4=0,
当λ=-$\frac{1}{4}$时,x=2满足题意,由于△>0,2是方程的根,∴$\frac{16λ-4}{1+4λ}$<0,
解得-$\frac{1}{4}$<λ<$\frac{1}{4}$时,方程两根异号,满足题意;
y=-2x-4代入方程x2+λy2=1,整理可得(1+4λ)x2+16λx+16λ-4=0
当λ=-$\frac{1}{4}$时,x=-2满足题意,由于△>0,-1是方程的根,∴$\frac{16λ-4}{1+4λ}$<0,
解得-$\frac{1}{4}$<λ<$\frac{1}{4}$时,方程两根异号,满足题意;
∵λ<0,∴实数λ的取值范围是[-$\frac{1}{4}$,0).
故答案为[-$\frac{1}{4}$,0).
点评 本题考查椭圆的简单几何性质,考查分类讨论的数学思想和不等式的解法以及数形结合,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知集合$A=\left\{{x|0≤x<1}\right\},B=\left\{{x|\frac{1}{x}≥1}\right\}$,则A∪B=( )
| A. | R | B. | [0,+∞) | C. | [0,1] | D. | (0,1) |
7.我们知道:在平面内,点(x0,y0)到直线Ax+By+C=0的距离公式为d=$\frac{{|{A{x_0}+B{y_0}+C}|}}{{\sqrt{{A^2}+{B^2}}}}$,通过类比的方法,可求得:在空间中,点(2,4,1)到直线x+2y+2z+3=0的距离为( )
| A. | 3 | B. | 5 | C. | $\frac{{5\sqrt{21}}}{7}$ | D. | $3\sqrt{5}$ |
4.已知α,β是两个不重合的平面,m,n是两条不同的直线,则下列命题中正确的是( )
| A. | 若m∥α,m∥β,则α∥β | B. | 若m∥n,m∥α,则n∥α | ||
| C. | 若α⊥β,m⊥α,n⊥β,则m⊥n | D. | 若α⊥β,m⊥α,n∥β,则m∥n |
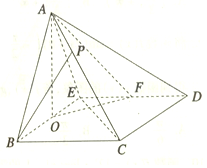 在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.
在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC. 如图所示,已知ABCD是直角梯形,∠BAD=90°,AD∥BC,AD=2AB=2BC,PA⊥面ABCD.
如图所示,已知ABCD是直角梯形,∠BAD=90°,AD∥BC,AD=2AB=2BC,PA⊥面ABCD.