题目内容
定义在R上的函数f(x),对任意两个不等的实数a,b,总有
>0成立,则f(x)必定是( )
| f(a)-f(b) |
| a-b |
| A、先增后减的函数 |
| B、先减后增的函数 |
| C、在R上的增函数 |
| D、在R上的减函数 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:解不等式
>0,得到a>b时,f(a)>f(b),或者a<b时,f(a)<f(b),从而得到函数的单调性.
| f(a)-f(b) |
| a-b |
解答:
解:由题意得:a>b时,f(a)>f(b),
或者a<b时,f(a)<f(b),
∴函数f(x)在R上是增函数,
故选:C.
或者a<b时,f(a)<f(b),
∴函数f(x)在R上是增函数,
故选:C.
点评:本题考查了函数的单调性,考查了导数的意义,是一道基础题.

练习册系列答案
相关题目
设a=log23,b=log32,c=log2(log32),则( )
| A、c<b<a |
| B、b<a<c |
| C、b<c<a |
| D、c<a<b |
已知数列{an}是等差数列,且a3+a4+a5+a6+a7=160,则a1+a9=( )
| A、32 | B、64 | C、96 | D、128 |
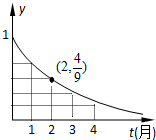 如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(a>0,a≠1,t≥0),有以下叙述:
如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(a>0,a≠1,t≥0),有以下叙述: 在平面上,
在平面上,