题目内容
已知数列{an}是等差数列，且a3+a4+a5+a6+a7=160，则a1+a9=（ ）
| A、32 | B、64 | C、96 | D、128 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：根据题意中等差数列的连续五项之和的值，利用等差中项做出第五项的值，要求的两项的和等于第五项的二倍，代入数值得到结果．
解答：
解：由等差数列的性质可得a3+a4+a5+a6+a7=5a5=160，
解得a5=32，
∴a1+a9=2a5=64
故选：B
解得a5=32，
∴a1+a9=2a5=64
故选：B
点评：本题考查等差中项的性质，本题解题的关键是写出等差中项的值，本题是一个基础题．
练习册系列答案
相关题目
已知cosθ＜0，那么角θ是（ ）
| A、第一或第二象限角 |
| B、第三或第四象限角 |
| C、第二或第三象限角 |
| D、第一或第四象限角 |
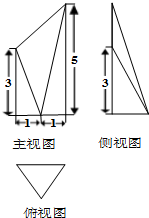已知某几何体的三视图如图所示，其中俯视图是边长为2的正三角形，侧视图是直角三角形，则此几何体的体积为（ ）A、
| ||||
B、
| ||||
C、8
| ||||
D、
|
定义在R上的函数f（x），对任意两个不等的实数a，b，总有
＞0成立，则f（x）必定是（ ）
| f(a)-f(b) |
| a-b |
| A、先增后减的函数 |
| B、先减后增的函数 |
| C、在R上的增函数 |
| D、在R上的减函数 |
函数f（x）=sin（2x+φ）（|φ＜
|）的图象向左平移
个单位后关于原点对称，求函数f（x）在[0，
]上的最小值为（ ）
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|