题目内容
若a＞b＞0，求证：aabb＞abba．
考点：不等式的证明
专题：证明题,函数的性质及应用,不等式的解法及应用
分析：运用作商法，再由指数函数的单调性，即可证明．
解答：
证明：
=（
）a•（
）b
=(
)a-b，
由于a＞b＞0，则a-b＞0，
＞1．
即有(
)a-b＞（
）0=1，
则有aabb＞abba．
| aabb |
| abba |
| a |
| b |
| b |
| a |
=(
| a |
| b |
由于a＞b＞0，则a-b＞0，
| a |
| b |
即有(
| a |
| b |
| a |
| b |
则有aabb＞abba．
点评：本题考查不等式的证明，考查作商法比较大小，考查指数函数的单调性和运用，属于中档题．
练习册系列答案
相关题目
已知向量
=(1，x2)，
=(x，8)，若
∥
，则实数x的值为（ ）
| a |
| b |
| a |
| b |
| A、2 | B、-2 | C、±2 | D、0 |
定义在R上的函数f（x），对任意两个不等的实数a，b，总有
＞0成立，则f（x）必定是（ ）
| f(a)-f(b) |
| a-b |
| A、先增后减的函数 |
| B、先减后增的函数 |
| C、在R上的增函数 |
| D、在R上的减函数 |
在正方体ABCD-A1B1C1D1中，E、F分别为AB、BC中点，则异面直线EF与AB1所成角的余弦值为（ ）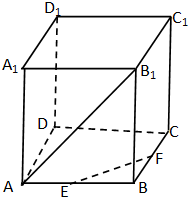
A、
| ||||
B、
| ||||
C、
| ||||
D、
|