题目内容
过椭圆
+
=1的焦点F的弦中最短弦长是 .
| x2 |
| 16 |
| y2 |
| 9 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:对于椭圆,过焦点的弦中垂直于x轴的弦最短,所以x=±
,带入椭圆方程即可求出对应y值,从而求出最短的弦长.
| 7 |
解答:
解:由题意设F(
,0),过F的弦中垂直于x轴的弦最短;
∴x=
时,y=±
;
∴最短弦长为
.
故答案为:
.
| 7 |
∴x=
| 7 |
| 9 |
| 4 |
∴最短弦长为
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |
点评:考查椭圆的标准方程,椭圆的焦点,弦的概念,以及过焦点的弦中垂直于x轴的弦最短.

练习册系列答案
相关题目
已知向量
=(1,x2),
=(x,8),若
∥
,则实数x的值为( )
| a |
| b |
| a |
| b |
| A、2 | B、-2 | C、±2 | D、0 |
设集合P={x|x≤3},则下列四个关系中正确的是( )
| A、0∈P | B、0∉P |
| C、{0}∈P | D、0⊆P |
定义在R上的函数f(x),对任意两个不等的实数a,b,总有
>0成立,则f(x)必定是( )
| f(a)-f(b) |
| a-b |
| A、先增后减的函数 |
| B、先减后增的函数 |
| C、在R上的增函数 |
| D、在R上的减函数 |
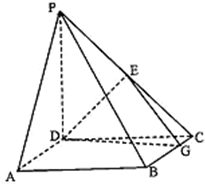 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,CB=3CG
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,CB=3CG