题目内容
设函数y=-2cos(
x+
),x∈[
π,a],若该函数是单调函数,求实数a的最大值.
| 1 |
| 2 |
| π |
| 3 |
| 28 |
| 5 |
考点:余弦函数的单调性
专题:三角函数的图像与性质
分析:两个相邻极值点对应的区间是单调区间,由于函数是单调函数.那么所给的区间[
,a]必是两个相邻极值点对应的区间的子区间.利用
,确定它的左右极值点,那么a≤右极值点对应的x值.
| 28π |
| 5 |
| 28π |
| 5 |
解答:
解:y=-2cos(
x+
)取极小值时,x=4kπ-
,k∈Z.
且 6π-
<
π<8π-
该函数是单调函数,所以a≤8π-
=
即a的最大值为
.
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
且 6π-
| 2π |
| 3 |
| 28 |
| 5 |
| 2π |
| 3 |
该函数是单调函数,所以a≤8π-
| 2π |
| 3 |
| 22π |
| 3 |
即a的最大值为
| 22π |
| 3 |
点评:本题主要考察了余弦函数的单调性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
定义在R上的函数f(x),对任意两个不等的实数a,b,总有
>0成立,则f(x)必定是( )
| f(a)-f(b) |
| a-b |
| A、先增后减的函数 |
| B、先减后增的函数 |
| C、在R上的增函数 |
| D、在R上的减函数 |
函数f(x)=sin(2x+φ)(|φ<
|)的图象向左平移
个单位后关于原点对称,求函数f(x)在[0,
]上的最小值为( )
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角的余弦值为( )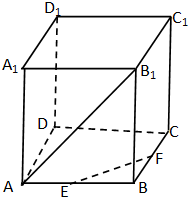

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=(
)x-x3-2的零点个数是( )
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |