Question

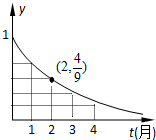如图，是某受污染的湖泊在自然净化过程中，某种有害物质的剩留量y与净化时间t（月）的近似函数关系：y=a^t（a＞0，a≠1，t≥0），有以下叙述：
①第4个月时，剩留量就会低于

1

5

；
②每月减少的有害物质量都相等；
③若剩留量为

1

2

， 

1

4

， 

1

8

所经过的时间分别是t₁，t₂，t₃，则t₁+t₂=t₃
其中所有正确的叙述是

 

．

Answer 1

考点：指数函数的图像与性质

专题：函数的性质及应用

分析：先根据图象经过点（2，

4

9

）求出a，然后对没有个选支进行逐一判断即可．

解答： 解：根据图象过点（2，

4

9

）可知
点（2，

4

9

）适合y=a^t即

4

9

=a²，
解得a=

2

3

，a=-

2

3

（舍去）
∴函数关系是y=(

2

3

)t，
令t=4时，y=

16

81

＜

1

5

，故①正确；
当t=1时，y=

2

3

，减少

1

3

，当t=2时，y=

4

9

，减少

2

9

，每月减少有害物质量不相等，故②不正确；
分别令y=

1

2

， 

1

4

， 

1

8

，解得t₁=log

2

3

1

2

，t₂=log

2

3

1

4

，t₃=log

2

3

1

8

，t₁+t₂=t₃，故③正确．
其中所有正确命题的序号是：①③
故答案为．①③

点评：本题考查的知识点是指数函数的综合应用、指数函数与幂函数的增长差异、函数的图象等知识，其中根据图象，确定函数图象经过的点的坐标，求出函数的解析式是解答本题的关键．