题目内容
在平面正六边形ABCDEF中，任选3个点，则3点构成的任意两条线段都成60°角概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：概率与统计
分析：计算出在平面正六边形ABCDEF中，任选3个点的取法个数，和满足条件“3点构成的任意两条线段都成60°角”的取法个数，代入古典概型概率计算公式，可得答案．
解答：
解：在平面正六边形ABCDEF中，任选3个点，有
=20种取法，
而3点构成的任意两条线段都成60°角，
即3点构成等边三角形，
有△ACE，△BDF两种情况，
则p=
=
，
故选B；
| C | 3 6 |
而3点构成的任意两条线段都成60°角，
即3点构成等边三角形，
有△ACE，△BDF两种情况，
则p=
| 2 |
| 20 |
| 1 |
| 10 |
故选B；
点评：本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．
练习册系列答案
相关题目
已知x＞0，y＞0，
+
=1．若x+2y＞m2-2m恒成立，则实数m的取值范围是（ ）
| 2 |
| x |
| 1 |
| y |
| A、m≥4或m≤-2 |
| B、-2＜m＜4 |
| C、m≥2或m≤-4 |
| D、-4＜m＜2 |
已知定义在R上的奇函数f（x）满足f（x+2e）=-f（x）（其中e=2.7182…），且在区间[e，2e]上是减函数，令a=
，b=
，c=
，则f（a），f（b），f（c） 的大小关系（用不等号连接）为（ ）
| ln2 |
| 2 |
| ln3 |
| 3 |
| ln5 |
| 5 |
| A、f（b）＞f（a）＞f（c） |
| B、f（b）＞f（c）＞f（a） |
| C、f（a）＞f（b）＞f（c） |
| D、f（a）＞f（c）＞f（b） |
已知实数集合M={x|
+
=1}，N={y|y=sinx，x∈M}，则M∩N=（ ）
| x2 |
| 9 |
| y2 |
| 4 |
| A、[-3，3] |
| B、[-1，1] |
| C、（-1，1） |
| D、[-sin3，sin3] |
用反证法证明命题“假设三角形内角至多少有一个不大于60°”时，反设正确的是（ ）
| A、假设三角形内角都不大于60° |
| B、假设三角形内角都大于60° |
| C、假设三角形内角至多少有一个大于60° |
| D、假设三角形内角至多少有两个大于60° |
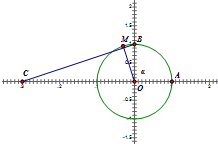如图，A、B是单位圆与x轴、y轴正半轴的交点，点M在单位圆上，∠AOM=α（0＜α＜π），点C（-3，0），若BC⊥OM，则sin（2α-| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个不透明的盒子里有质地、大小完全相同的5个球，编号分别为1，2，3，4，5，甲、乙两人玩一种游戏：甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，如果两个编号的和为偶数算甲赢，否则算乙赢．那么甲赢的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
| D、以上均不对 |
以圆 （x-1）2+y2=2的圆心为抛物线的焦点，且顶点为坐标原点的抛物线方程为（ ）
| A、y2=4x |
| B、y2=2x |
| C、x2=4y |
| D、x2=2y |