题目内容
用根式表示下列各式:
(1)a
= ; (2)b
= ;(3)a
= ;(4)c -
= ;(5)e -
= .
(1)a
| 1 |
| 2 |
| 3 |
| 4 |
| 7 |
| 5 |
| 2 |
| 3 |
| 4 |
| 5 |
考点:方根与根式及根式的化简运算
专题:常规题型,计算题
分析:利用负分数指数幂、正分数指数幂与根式的转换关系求解
解答:
解:根据公式a
=
,a -
=
计算得到:(1)a
=
; (2)b
=
;(3)a
=
;(4)c -
=
;(5)e -
=
| m |
| n |
| n | am |
| m |
| n |
| 1 | |||
|
| 1 |
| 2 |
| a |
| 3 |
| 4 |
| 4 | b3 |
| 7 |
| 5 |
| 5 | a7 |
| 2 |
| 3 |
| 1 | |||
|
| 4 |
| 5 |
| 1 | |||
|
点评:考查了分数指数幂的概念,及与根式转换关系,是基本的运算题目

练习册系列答案
相关题目
已知A,B是圆心为C,半径为
的圆上两点,且|
|=
,则
•
等于( )
| 5 |
| AB |
| 5 |
| AC |
| CB |
A、-
| ||||
B、
| ||||
| C、0 | ||||
D、
|
定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,4)时,f(x)=2x,则f(sin1)与f(cos1)的大小关系为( )
| A、f(sin1)<f(cos1) |
| B、f(sin1)=f(cos1) |
| C、f(sin1)>f(cos1) |
| D、不确定 |
已知数列{an}的前n项和为Sn=1-5+9-13+17-21+…+(-1)n+1(4n-3),则S15+S22-S31的值是( )
| A、-76 | B、76 | C、46 | D、13 |
在平面正六边形ABCDEF中,任选3个点,则3点构成的任意两条线段都成60°角概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
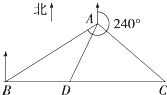 海上一观测站测得方位角240°的方向上有一艘停止待修的商船,在商船的正东方有一艘海盗船正向它靠近,速度为每小时90海里.此时海盗船距观测站10
海上一观测站测得方位角240°的方向上有一艘停止待修的商船,在商船的正东方有一艘海盗船正向它靠近,速度为每小时90海里.此时海盗船距观测站10