题目内容
偶函数f(x)在[0,+∞)上为增函数,若不等式f(ax-1)<f(2+x2)恒成立,则实数a的取值范围是 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据偶函数图象关于y轴对称,得f(x)在[0,+∞)上单调增,且在(-∞,0]上是单调减函数,由此结合2+x2是正数,将原不等式转化为|ax-1|<2+x2恒成立,去绝对值再用一元二次不等式恒成立的方法进行处理,即得实数a的取值范围.
解答:
解:∵f(x)是偶函数,图象关于y轴对称.
∴f(x)在(-∞,0)上的单调性与[0,+∞)的单调性相反,可得f(x)在(-∞,0]上是减函数.
∴不等式f(ax-1)<f(2+x2)恒成立,等价于|ax-1|<2+x2恒成立,
即不等式-2-x2<ax-1<2+x2恒成立,整理得
的解集为R,
∴结合一元二次方程根的判别式,得:a2-4<0且(-a)2-12<0,
解之得-2<a<2;
故答案为:-2<a<2.
∴f(x)在(-∞,0)上的单调性与[0,+∞)的单调性相反,可得f(x)在(-∞,0]上是减函数.
∴不等式f(ax-1)<f(2+x2)恒成立,等价于|ax-1|<2+x2恒成立,
即不等式-2-x2<ax-1<2+x2恒成立,整理得
|
∴结合一元二次方程根的判别式,得:a2-4<0且(-a)2-12<0,
解之得-2<a<2;
故答案为:-2<a<2.
点评:本题给出偶函数的单调性,解决关于x的不等式恒成立的问题,着重考查了函数的单调性与奇偶性、一元二次不等式解法等知识.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
当a>0时,函数f(x)=(x2-ax)ex的图象大致是( )
A、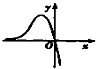 |
B、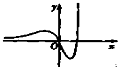 |
C、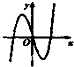 |
D、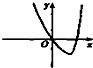 |