题目内容
已知D为△ABC中BC边上的点,且满足∠BAD=60°,∠CAD=45°,AB=
,AC=
,则
= .
| 2 |
| 3 |
| BD |
| CD |
考点:正弦定理
专题:计算题,解三角形
分析:在三角形ABD中和三角形ACD中,运用正弦定理,再两式相除,运用诱导公式,即可得到.
解答:
解:在三角形ABD中,
=
,①
在三角形ACD中,
=
,②
由于sin∠ADB=sin∠ADC,
则①÷②,得
•
=
,即有
=1.
故答案为:1.
| BD |
| sin60° |
| AB |
| sin∠ADB |
在三角形ACD中,
| CD |
| sin45° |
| AC |
| sin∠ADC |
由于sin∠ADB=sin∠ADC,
则①÷②,得
| BD |
| CD |
| ||
|
| ||
|
| BD |
| CD |
故答案为:1.
点评:本题考查解三角形中的正弦定理及运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
函数y=ax2+bx+c与y=ax+b(ab≠0)的图象可能是( )
A、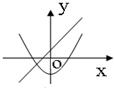 |
B、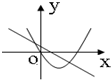 |
C、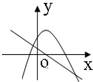 |
D、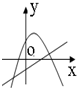 |
f(x)=
,则f[f(
)]( )
|
| 1 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
| D、D、 |