题目内容
函数y=ax2+bx+c与y=ax+b（ab≠0）的图象可能是（ ）
A、 |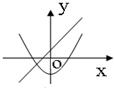
B、 |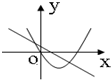
C、 |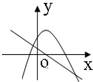
D、 |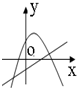
考点：函数的图象
专题：函数的性质及应用
分析：根据一次函数和二次函数的图象和性质，分别判断各选项是否相符即可
解答：
解：对于选项A，由直线y=ax+b得到a＞0，b＞0，则二次函数的对称轴为x=-
＜0，故A不符合，
对于选项B，由直线y=ax+b得到a＜0，b＞0，则y=ax2+bx+c开口向下，故B不符合，
对于选项C，由直线y=ax+b得到a＜0，b＞0，则二次函数的对称轴为x=-
＞0，故C符合，
对于选项D，由直线y=ax+b得到a＞0，b＜0，则y=ax2+bx+c开口向上，故D不符合，
故选：C
| b |
| 2a |
对于选项B，由直线y=ax+b得到a＜0，b＞0，则y=ax2+bx+c开口向下，故B不符合，
对于选项C，由直线y=ax+b得到a＜0，b＞0，则二次函数的对称轴为x=-
| b |
| 2a |
对于选项D，由直线y=ax+b得到a＞0，b＜0，则y=ax2+bx+c开口向上，故D不符合，
故选：C
点评：本题主要考查了二次函数和一次函数的图象和性质，属于基础题
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知底面边长为2，侧棱长为2
，则正四棱柱的各顶点均在同一个球面上，则该球的体积为（ ）
| 2 |
A、
| ||
| B、4π | ||
| C、2π | ||
D、
|
