题目内容

6．某四面体的三视图如图所示，该四面体四个面的面积中，最大的是（　　）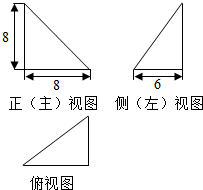
A．24B．24$\sqrt{2}$C．40D．20

分析 根据三视图得出该几何体是一个三棱锥，画出图形求出四个面的面积即可．

解答 解：根据三视图得出该几何体是一个三棱锥，如图所示：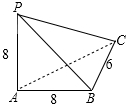

则四个面的面积分别为：S△PAB=$\frac{1}{2}$×8×8=32，
S△PAC=$\frac{1}{2}$×8×$\sqrt{{8}^{2}{+6}^{2}}$=40，
S△PBC=$\frac{1}{2}$×6×8$\sqrt{2}$=24$\sqrt{2}$，
S△ABC=$\frac{1}{2}$×8×6=24；
显然面积的最大值为40．
故选：C．

点评 本题考查了由三视图判断几何体的结构特征的应用问题，也考查了几何体的面积与空间想象能力的应用问题，是基础题目．

练习册系列答案
相关题目
7．已知函数f（x）=$\sqrt{3}$sinxcosx-sin2x-$\frac{1}{2}$，x∈[0，$\frac{π}{2}$]，则函数f（x）的值域为[-2，0]．
8．已知函数f（x）=$\left\{\begin{array}{l}{l{n}^{2}x+alnx+b，x＞0}\\{{e}^{x}+\frac{1}{4}，x≤0}\end{array}\right.$，且f（e）=f（1），f（e2）=f（0）+$\frac{11}{4}$，则不等式f（lnx）≥1的解集是（　　）
A．{x|x$≥\frac{7}{4}$}B．{x|$\frac{3}{4}$≤x≤1}C．{x|$\frac{3}{4}$≤x≤$\frac{7}{4}$}D．{x|x≥$\frac{3}{4}$}
5．五边形ABCDE为正五边形，以A，B，C，D，E为顶点的三角形的个数是（　　）
A．5B．10C．15D．20
1．化简$\frac{2sin2α}{1+cos2α}$•$\frac{co{s}^{2}α}{cos2α}$=（　　）
A．tanαB．tan2αC．1D．$\frac{1}{2}$
11．设定义在R上的函数f（x）对任意实数x满足f（x）=f（x-2）+3，且f（2）=4，则f（6）=10．
18．已知两点A（1，0），B（1，$\sqrt{3}$），O为坐标原点，点C在第二象限，且∠AOC=150°，设$\overrightarrow{OC}=λ\overrightarrow{OA}+2\overrightarrow{OB}$，（λ∈R），则λ=-8．
15．函数f（x）=$\sqrt{2}sinx•cos（x+\frac{π}{4}）$，则$f（\frac{π}{2}）$=-1，f（x）的值域是$[-\frac{{\sqrt{2}+1}}{2}，\frac{{\sqrt{2}-1}}{2}]$．
16．已知$cos（{60°}+α）=\frac{1}{3}$，且-180°＜α＜-90°，则cos（30°-α）的值为（　　）
A．$-\frac{{2\sqrt{2}}}{3}$B．$\frac{{2\sqrt{2}}}{3}$C．$-\frac{{\sqrt{2}}}{3}$D．$\frac{{\sqrt{2}}}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网