题目内容
18.已知两点A(1,0),B(1,$\sqrt{3}$),O为坐标原点,点C在第二象限,且∠AOC=150°,设$\overrightarrow{OC}=λ\overrightarrow{OA}+2\overrightarrow{OB}$,(λ∈R),则λ=-8.分析 根据向量的基本运算表示出C的坐标,利用三角函数的定义进行求解即可.
解答 解:$\overrightarrow{OC}=λ\overrightarrow{OA}+2\overrightarrow{OB}$=λ(1,0)+2(1,$\sqrt{3}$)=(λ+2,2$\sqrt{3}$),即C(λ+2,2$\sqrt{3}$),
∵∠AOC=150°,
∴tan150°=$\frac{2\sqrt{3}}{λ+2}$=-$\frac{\sqrt{3}}{3}$,
即λ+2=-6,
即λ=-8,
故答案为:-8
点评 本题主要考查向量坐标的应用以及三角函数的定义,根据向量的基本运算求出C的坐标是解决本题的关键.

练习册系列答案
相关题目
20.已知集合A={y|y=x${\;}^{\frac{1}{3}}$,-1≤x≤1},B={y|y=2-$\frac{1}{x}$,0<x≤1},则集合A∪B=( )
| A. | (-∞,1] | B. | [-1,1] | C. | ∅ | D. | {1} |
6.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( )
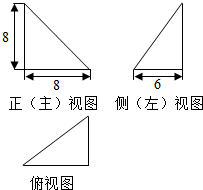

| A. | 24 | B. | 24$\sqrt{2}$ | C. | 40 | D. | 20 |
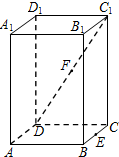 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: