题目内容
1.化简$\frac{2sin2α}{1+cos2α}$•$\frac{co{s}^{2}α}{cos2α}$=( )| A. | tanα | B. | tan2α | C. | 1 | D. | $\frac{1}{2}$ |
分析 直接利用二倍角公式化1+cos2α为2cos2α,约分后利用商的关系得答案.
解答 解:$\frac{2sin2α}{1+cos2α}$•$\frac{co{s}^{2}α}{cos2α}$=$\frac{2sin2α}{2co{s}^{2}α}•\frac{co{s}^{2}α}{cos2α}$=tan2α.
故选:B.
点评 本题考查三角函数的化简求值,考查了同角三角函数的基本关系式,是基础题.

练习册系列答案
相关题目
20.已知集合A={y|y=x${\;}^{\frac{1}{3}}$,-1≤x≤1},B={y|y=2-$\frac{1}{x}$,0<x≤1},则集合A∪B=( )
| A. | (-∞,1] | B. | [-1,1] | C. | ∅ | D. | {1} |
6.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( )
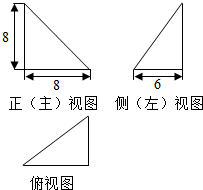

| A. | 24 | B. | 24$\sqrt{2}$ | C. | 40 | D. | 20 |
11.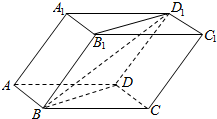 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{3}{4}$ |
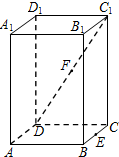 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: