题目内容
16.已知$cos({60°}+α)=\frac{1}{3}$,且-180°<α<-90°,则cos(30°-α)的值为( )| A. | $-\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
分析 由cos(60°+α)的值及α的范围,判断出sin(60°+α)的正负,进而求出sin(60°+α)的值,原式变形后利用诱导公式化简即可求出值.
解答 解:∵cos(60°+α)=$\frac{1}{3}$,-180°<α<-90°,即-120°<α+60°<-30°,
∴sin(60°+α)<0,即sin(60°+α)=-$\sqrt{1-(\frac{1}{3})^{2}}$=-$\frac{2\sqrt{2}}{3}$,
则原式=cos[90°-(60°+α)]=sin(60°+α)=-$\frac{2\sqrt{2}}{3}$,
故选:A.
点评 此题考查了运用诱导公式化简求值,以及同角三角函数间的基本关系,熟练掌握诱导公式及基本关系是解本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
6.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( )
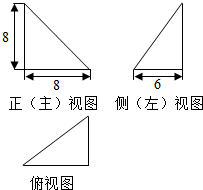

| A. | 24 | B. | 24$\sqrt{2}$ | C. | 40 | D. | 20 |
4.已知函数f(x)=ax2+bx+3a+b为偶函数,其定义域为[a-3,2a],则a+b的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
11.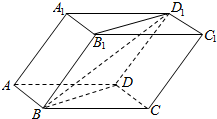 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{3}{4}$ |
5.下列说法错误的是( )
| A. | 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系 | |
| B. | 在线性回归分析中,相关系数r的值越大,变量间的相关性越强 | |
| C. | 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高 | |
| D. | 在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好 |
6.函数$f(x)=\frac{{\root{3}{3x+5}}}{{a{x^2}+4ax+3}}$的定义域为R,则实数a的取值范围是( )
| A. | (-∞,+∞) | B. | $(0,\frac{3}{4})$ | C. | $(\frac{3}{4},+∞)$ | D. | $[0,\frac{3}{4})$ |