题目内容
7.已知函数f(x)=$\sqrt{3}$sinxcosx-sin2x-$\frac{1}{2}$,x∈[0,$\frac{π}{2}$],则函数f(x)的值域为[-2,0].分析 先利用三角函数的倍角公式和两角和公式对函数进行化简得f(x)=sin(2x+$\frac{π}{6}$),然后求出函数的值域.
解答 解:∵x∈[0,$\frac{π}{2}$],
∴f(x)=$\sqrt{3}$sinxcosx-sin2x-$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}sin2x$+$\frac{1}{2}cos2x$-1
=sin(2x+$\frac{π}{6}$)-1.
∴函数f(x)的值域为[-2,0].
故答案为:[-2,0].
点评 本题主要二倍角公式的应用,两角和与差的三角函数,正弦函数的性质的应用,考查函数y=Asin(ωx+φ)的图象变换,属中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
6.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( )
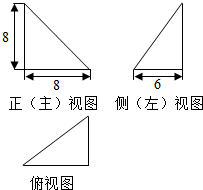

| A. | 24 | B. | 24$\sqrt{2}$ | C. | 40 | D. | 20 |