题目内容
15.函数f(x)=$\sqrt{2}sinx•cos(x+\frac{π}{4})$,则$f(\frac{π}{2})$=-1,f(x)的值域是$[-\frac{{\sqrt{2}+1}}{2},\frac{{\sqrt{2}-1}}{2}]$.分析 利用余弦加法定理、二倍角公式和三角函数恒等式求出f(x)=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)-$\frac{1}{2}$,由此能求出f($\frac{π}{3}$)和f(x)的值域.
解答 解:∵f(x)=$\sqrt{2}sinx•cos(x+\frac{π}{4})$
=$\sqrt{2}sinx$(cosxcos$\frac{π}{4}$-sinxsin$\frac{π}{4}$)
=sinx(cosx-sinx)
=sinxcosx-sin2x
=$\frac{1}{2}sin2x$-$\frac{1-cos2x}{2}$
=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)-$\frac{1}{2}$,
∴$f(\frac{π}{2})$=$\frac{\sqrt{2}}{2}sin(π+\frac{π}{4})-\frac{1}{2}$=-$\frac{\sqrt{2}}{2}•\frac{\sqrt{2}}{2}$-$\frac{1}{2}$=-1.
f(x)=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)-$\frac{1}{2}$的值域为$[-\frac{{\sqrt{2}+1}}{2},\frac{{\sqrt{2}-1}}{2}]$.
故答案为:-1,$[-\frac{{\sqrt{2}+1}}{2},\frac{{\sqrt{2}-1}}{2}]$.
点评 本题考查三角函数的值域的求法,是中档题,解题时要认真审题,注意余弦加法定理、二倍角公式和三角函数恒等式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( )
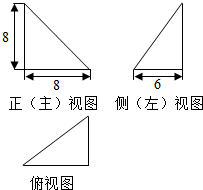

| A. | 24 | B. | 24$\sqrt{2}$ | C. | 40 | D. | 20 |
4.已知函数f(x)=ax2+bx+3a+b为偶函数,其定义域为[a-3,2a],则a+b的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
5.下列说法错误的是( )
| A. | 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系 | |
| B. | 在线性回归分析中,相关系数r的值越大,变量间的相关性越强 | |
| C. | 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高 | |
| D. | 在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好 |
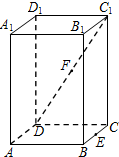 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: