题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{l{n}^{2}x+alnx+b,x>0}\\{{e}^{x}+\frac{1}{4},x≤0}\end{array}\right.$,且f(e)=f(1),f(e2)=f(0)+$\frac{11}{4}$,则不等式f(lnx)≥1的解集是( )| A. | {x|x$≥\frac{7}{4}$} | B. | {x|$\frac{3}{4}$≤x≤1} | C. | {x|$\frac{3}{4}$≤x≤$\frac{7}{4}$} | D. | {x|x≥$\frac{3}{4}$} |
分析 由题意,$\left\{\begin{array}{l}{1+a+b=b}\\{4+2a+b=4}\end{array}\right.$,可得a=-1,b=2,再分类讨论,即可求出不等式f(lnx)≥1的解集.
解答 解:由题意,$\left\{\begin{array}{l}{1+a+b=b}\\{4+2a+b=4}\end{array}\right.$,∴a=-1,b=2,
lnx≤0,则x+$\frac{1}{4}$≥1,∴x≥$\frac{3}{4}$,∴$\frac{3}{4}$≤x≤1;
lnx>0,f(lnx)=(lnlnx-$\frac{1}{2}$)2+$\frac{7}{4}$>1恒成立,∴x>1,
综上,x≥$\frac{3}{4}$.
故选:D.
点评 本题考查分段函数,考查求不等式f(lnx)≥1的解集,求出a,b是关键.

练习册系列答案
相关题目
20.已知集合A={y|y=x${\;}^{\frac{1}{3}}$,-1≤x≤1},B={y|y=2-$\frac{1}{x}$,0<x≤1},则集合A∪B=( )
| A. | (-∞,1] | B. | [-1,1] | C. | ∅ | D. | {1} |
6.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( )
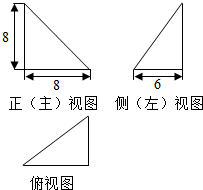

| A. | 24 | B. | 24$\sqrt{2}$ | C. | 40 | D. | 20 |