题目内容
11.设定义在R上的函数f(x)对任意实数x满足f(x)=f(x-2)+3,且f(2)=4,则f(6)=10.分析 利用f(x)=f(x-2)+3,且f(2)=4,将f(6)逐步转化到f(2)上来,求解即可.
解答 解:因为函数f(x)对任意实数x满足f(x)=f(x-2)+3,且f(2)=4,
f(4)=f(4-2)+3=f(2)+3=4+3=7.
所以f(6)=f(6-2)+3=f(4)+3=7+3=10.
故答案为:10.
点评 本题考查了抽象函数问题,要仔细体会f(x)=f(x-2)+3在求值中的作用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( )
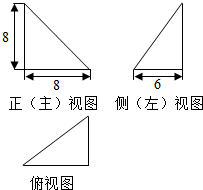

| A. | 24 | B. | 24$\sqrt{2}$ | C. | 40 | D. | 20 |