题目内容
P为圆A:(x+1)2+y2=8上的动点,点B(1,0).线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
(I)求曲线Γ的方程;
(Ⅱ)当点P在第一象限,且cos∠BAP=
时,求点M的坐标.
(I)求曲线Γ的方程;
(Ⅱ)当点P在第一象限,且cos∠BAP=
2
| ||
| 3 |
考点:直线和圆的方程的应用
专题:综合题,直线与圆,圆锥曲线的定义、性质与方程
分析:(I)由已知|MB|=|MP|,于是|MA|+|MB|=|MA|+|MP|=2
,故曲线Γ是以A,B为焦点,以2
为长轴长的椭圆,从而可求曲线Γ的方程;
(Ⅱ)当点P在第一象限,且cos∠BAP=
时,求出P的坐标,可得直线AP方程,代入椭圆方程,消去y,可得5x2+2x-7=0,即可求点M的坐标.
| 2 |
| 2 |
(Ⅱ)当点P在第一象限,且cos∠BAP=
2
| ||
| 3 |
解答:
解:(Ⅰ)圆A的圆心为A(-1,0),半径等于2
.
由已知|MB|=|MP|,于是|MA|+|MB|=|MA|+|MP|=2
,
故曲线Γ是以A,B为焦点,以2
为长轴长的椭圆,a=
,c=1,b=1,
曲线Γ的方程为
+y2=1.…(5分)
(Ⅱ)由点P在第一象限,cos∠BAP=
,|AP|=2
,得P(
,
).…(8分)
于是直线AP方程为y=
(x+1).
代入椭圆方程,消去y,可得5x2+2x-7=0,
所以x1=1,x2=-
.
由于点M在线段AP上,所以点M坐标为(1,
).…(12分)
| 2 |
由已知|MB|=|MP|,于是|MA|+|MB|=|MA|+|MP|=2
| 2 |
故曲线Γ是以A,B为焦点,以2
| 2 |
| 2 |
曲线Γ的方程为
| x2 |
| 2 |
(Ⅱ)由点P在第一象限,cos∠BAP=
2
| ||
| 3 |
| 2 |
| 5 |
| 3 |
2
| ||
| 3 |
于是直线AP方程为y=
| ||
| 4 |
代入椭圆方程,消去y,可得5x2+2x-7=0,
所以x1=1,x2=-
| 7 |
| 5 |
由于点M在线段AP上,所以点M坐标为(1,
| ||
| 2 |
点评:本题考查直线与圆的位置关系,考查椭圆的方程与定义,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知方程
=k在(0,+∞)上有两个不同的解α,β(α<β),则下面结论正确的是( )
| |sinx| |
| x |
| A、sinα=αcosβ |
| B、sinα=-αcosβ |
| C、cosα=βsinβ |
| D、sinβ=-βsinα |
对于实数a和b,定义运算a*b,运算原理如图所示,则式子(
)-2*lne2的值为( )
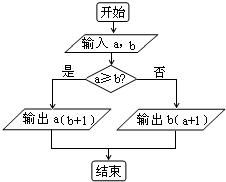
| 1 |
| 2 |

| A、8 | ||
| B、10 | ||
| C、12 | ||
D、
|
若0<x<y<1,则( )
| A、logx3<logy3 | ||||
| B、3y<3x | ||||
| C、log4x<log4y | ||||
D、(
|