题目内容
已知方程
=k在(0,+∞)上有两个不同的解α,β(α<β),则下面结论正确的是( )
| |sinx| |
| x |
| A、sinα=αcosβ |
| B、sinα=-αcosβ |
| C、cosα=βsinβ |
| D、sinβ=-βsinα |
考点:函数的图象与图象变化
专题:数形结合,转化思想,函数的性质及应用
分析:方程
=k有两个根,即函数y=|sinx|和函数y=kx在(0,+∞)上有两个交点,画出函数图象,利用导数求切线即可.
| |sinx| |
| x |
解答:
解:∵
=kx有两个根,∴函数y=|sinx|和函数y=kx在(0,+∞)上有两个交点,x>0且k>0,画出两个函数的图象,如图(1)
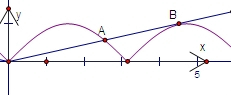
图1
函数y=|sinx|和函数y=kx在(0,π)上有一个交点A(α,sinα),在(π,2π)上有一个切点B(β,sinβ)时满足题意,α,β是方程的根.
当x∈(π,2π)时,f(x)=|sinx|=-sinx,f′(x)=-cosx,
∴在B处的切线为y-sinβ=f′(β)(x-β),将x=0,y=0代入方程,得sinβ=-βcosβ,
∴
=-cosβ,
∵O,A B三点共线,
∴
=
,
∴
=-cosβ,
∴sinα=-αcosβ.
故选:B.
| |sinx| |
| x |

图1
函数y=|sinx|和函数y=kx在(0,π)上有一个交点A(α,sinα),在(π,2π)上有一个切点B(β,sinβ)时满足题意,α,β是方程的根.
当x∈(π,2π)时,f(x)=|sinx|=-sinx,f′(x)=-cosx,
∴在B处的切线为y-sinβ=f′(β)(x-β),将x=0,y=0代入方程,得sinβ=-βcosβ,
∴
| sinβ |
| β |
∵O,A B三点共线,
∴
| -sinα |
| α |
| -sinβ |
| β |
∴
| sinα |
| α |
∴sinα=-αcosβ.
故选:B.
点评:本题借助图象考查了方程的根,函数的零点,以及导数的知识.把方程转化为函数的交点,数形结合是解题关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
设函数f(x)=sinxcosx,x∈R,则函数f(x)的最小值是( )
A、-
| ||||
B、-
| ||||
C、-
| ||||
| D、-1 |
空间中,α,β,γ是三个互不重合的平面,l是一条直线,则下列命题中正确的是( )
| A、若α⊥β,l∥α,则l⊥β |
| B、若α⊥β,l⊥β,则l∥α |
| C、若l⊥α,l∥β,则α⊥β |
| D、若l∥α,l∥β,则α∥β |
阅读如图的程序框图,则输出的S=( )


| A、7 | B、8 | C、15 | D、24 |
在△ABC中,若AB=2,AC=3,∠A=60°,则BC的长为( )
A、
| ||
B、
| ||
| C、3 | ||
D、
|
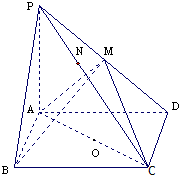 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.