题目内容
设集合M={x|x2-2x-3<0},N={x|log2(1-x)<1},则M∩∁RN等于( )
| A、[-1,1] |
| B、(-1,0) |
| C、[1,3) |
| D、(0,1) |
考点:交、并、补集的混合运算
专题:集合
分析:解一元二次不等式求得M,解对数不等式求得N,再根据补集的定义求得∁RN,利用两个集合的交集的定义求得M∩∁RN.
解答:
解:∵集合M={x|x2-2x-3<0}={x|-1<x<3},
N={x|log2(1-x)<1}={x|0<1-x<2}={x|-1<x<1},
∴∁RN={x|x≤-1,或 x≥1},∴M∩∁RN=[1,3),
故选:C.
N={x|log2(1-x)<1}={x|0<1-x<2}={x|-1<x<1},
∴∁RN={x|x≤-1,或 x≥1},∴M∩∁RN=[1,3),
故选:C.
点评:本题主要考查一元二次不等式的解法,对数不等式的解法,求集合的补集,两个集合的交集的定义和求法,属于基础题.

练习册系列答案
相关题目
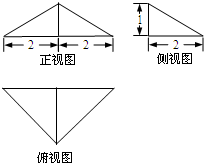
某三棱锥的三视图如图所示,则该几何体的体积为( )

A、
| ||
B、
| ||
C、
| ||
| D、4 |
已知下列四个命题:
①底面积和高均相等的柱体体积是锥体体积的3倍:
②正方体的截面是一个n边形,则n的最大值是6;
③在棱长为1的正方体ABCD-AB1C1D1中,三棱锥A1-ABC的体积是
;
④4条棱均为
的四面体的体积是
;
其中真命题的序号是( )
①底面积和高均相等的柱体体积是锥体体积的3倍:
②正方体的截面是一个n边形,则n的最大值是6;
③在棱长为1的正方体ABCD-AB1C1D1中,三棱锥A1-ABC的体积是
| 1 |
| 4 |
④4条棱均为
| 2 |
| 1 |
| 3 |
其中真命题的序号是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
设i为虚数单位,复数
在复平面上对应的点在( )
| 2+i |
| i2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设已知a,b,m均为整数(m>0),若a和b被m除所得的余数相同,则称a和b对模m同余,记为a≡b(modm),若a=C
+C
•2+C
•22+…+C
•240,且a≡b(mod10),则b的值可以是( )
0 40 |
1 40 |
3 40 |
40 40 |
| A、2011 | B、2012 |
| C、2013 | D、2014 |
二次函数y=ax2+bx与指数函数y=(-
)x的图象只可能是( )
| b |
| a |
A、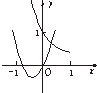 |
B、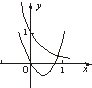 |
C、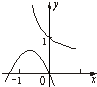 |
D、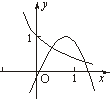 |