题目内容
一个几何体的三视图如图所示，则该几何体内切球的体积为 ．
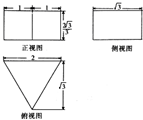
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得，该几何是一个以俯视图为底面的棱柱，根据已知中的棱长高等几何量，求出其内切球的半径，代入球的体积公式，可得答案．
解答：
解：由已知中的三视图可得，该几何是一个以俯视图为底面的棱柱，
∵底面是底边长为2，高为
的等腰三角形，
∴底面是边长为2的等边三角形，
又由棱柱的高为
，
故棱柱的内切球半径R=
，
故棱柱的内切球的体积V=
πR3=
，
故答案为：
．
∵底面是底边长为2，高为
| 3 |
∴底面是边长为2的等边三角形，
又由棱柱的高为
2
| ||
| 3 |
故棱柱的内切球半径R=
| ||
| 3 |
故棱柱的内切球的体积V=
| 4 |
| 3 |
4
| ||
| 27 |
故答案为：
4
| ||
| 27 |
点评：本题考查的知识点是由三视图求体积，其中分析出几何体的形状是解答的关键．
练习册系列答案
相关题目
设集合M={x|x2-2x-3＜0}，N={x|log2（1-x）＜1}，则M∩∁RN等于（ ）
| A、[-1，1] |
| B、（-1，0） |
| C、[1，3） |
| D、（0，1） |