题目内容
设已知a,b,m均为整数(m>0),若a和b被m除所得的余数相同,则称a和b对模m同余,记为a≡b(modm),若a=C
+C
•2+C
•22+…+C
•240,且a≡b(mod10),则b的值可以是( )
0 40 |
1 40 |
3 40 |
40 40 |
| A、2011 | B、2012 |
| C、2013 | D、2014 |
考点:二项式系数的性质
专题:二项式定理
分析:根据已知中a和b对模m同余的定义,结合二项式定理,我们可以求出a的值,结合a≡b(bmod10),比照四个答案中的数字,结合得到答案.
解答:
解:∵a=C
+C
•2+C
•22+…+C
•240,
(1+2)40=340=1+2C401+22C402+…+240C4040,
∴a=340.
∵31个位是3,32个位是9,33个位是7,34个位是1,35个位是3,…
∴340个位是1,
若a≡b(mod10),则b的个位也是1.
故选:A.
0 40 |
1 40 |
3 40 |
40 40 |
(1+2)40=340=1+2C401+22C402+…+240C4040,
∴a=340.
∵31个位是3,32个位是9,33个位是7,34个位是1,35个位是3,…
∴340个位是1,
若a≡b(mod10),则b的个位也是1.
故选:A.
点评:本题考查的知识点是同余定理,其中正确理解a和b对模m同余,是解答本题的关键,同时利用二项式定理求出a的值,也很关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
已知集合A={x|x2-1<0},B={x|x<m},若“a∈A”是“a∈B”的充分而不必要条件,则实数m的取值可以是( )
A、
| ||
B、
| ||
| C、1 | ||
D、
|
函数f(x)=2sin(2x-φ)(|φ|<
)的图象如图所示,则φ的值等于( )
| π |
| 2 |

A、
| ||
B、
| ||
C、-
| ||
D、-
|
设集合M={x|x2-2x-3<0},N={x|log2(1-x)<1},则M∩∁RN等于( )
| A、[-1,1] |
| B、(-1,0) |
| C、[1,3) |
| D、(0,1) |
已知一个几何体的三视图如图所示,根据图中尺寸可得该几何体的表面积为( )


A、12+4
| ||
| B、16 | ||
C、14+2
| ||
| D、20 |
已知函数f(x)=x2+2a1og2(x2+2)+a2-3有且只有一个零点,则实数a的值为( )
| A、1 | B、-3 | C、2 | D、1或-3 |
若向量
=(2,-1),
=(0,2),则以下向量中与
+
垂直的是( )
| a |
| b |
| a |
| b |
| A、(1,-2) |
| B、(1,2) |
| C、(2,1) |
| D、(0,2) |
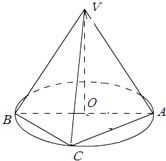 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,已知AB=2,VA=VB=VC=2.