题目内容
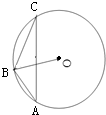
如图所示,△ABC的外接圆圆心为O,已知|
|=3,|
|=5,则
•
=
| AB |
| BC |
| OB |
| AC |

考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:设AB的中点为M,BC的中点为N,连接OC,OA,OM,ON,运用向量的三角形法则,结合向量的数量积的定义和解直角三角形的知识,以及圆的垂径定理,即可计算得到.
解答:
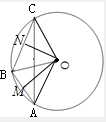 解:设AB的中点为M,BC的中点为N,
解:设AB的中点为M,BC的中点为N,
连接OC,OA,OM,ON,
则有OM⊥AB,ON⊥BC,
则
•
=
•(
-
)=-
•(
-
)
=
•
-
•
=|
|•|
|•cos∠OBA-|
|•|
|•cos∠OBC
=|
|•|
|-|
|•|
|=
(
2-
2)
=
×(9-25)=-8.
故答案为:-8.
 解:设AB的中点为M,BC的中点为N,
解:设AB的中点为M,BC的中点为N,连接OC,OA,OM,ON,
则有OM⊥AB,ON⊥BC,
则
| OB |
| AC |
| OB |
| BC |
| BA |
| BO |
| BC |
| BA |
=
| BO |
| BA |
| BO |
| BC |
| BO |
| BA |
| BO |
| BC |
=|
| BM |
| BA |
| BN |
| BC |
| 1 |
| 2 |
| BA |
| BC |
=
| 1 |
| 2 |
故答案为:-8.
点评:本题考查平面向量的数量积的定义和性质,考查圆的垂径定理及运用,考查运算能力,属于中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
已知点Q(0,3)及抛物线y2=16x上一动点P(x0,y0),则x0+|PQ|的最小值为( )
| A、1 | B、2 | C、4 | D、5 |
 在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=2,E是BC的中点,建立空间直角坐标系,用向量方法解决下列问题.
在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=2,E是BC的中点,建立空间直角坐标系,用向量方法解决下列问题.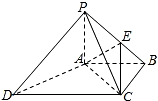 四棱锥P-ABCD中,DC∥AB,AB=2DC=4
四棱锥P-ABCD中,DC∥AB,AB=2DC=4