题目内容
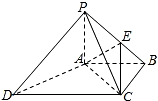 四棱锥P-ABCD中,DC∥AB,AB=2DC=4
四棱锥P-ABCD中,DC∥AB,AB=2DC=4| 5 |
(Ⅰ)证明:平面MAC⊥平面PAD;
(Ⅱ)若△PAD为等边三角形,平面MAC把四棱锥P-ABCD分成两个几何体,当着两个几何体的体积之比VM-ACD:VM-ABC=11:4时,求
| PM |
| MB |
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)由勾股定理可得AC⊥AD,进而由面面垂直的性质得到:AC⊥平面PAD,再由面面垂直的判定定理得到:平面MAC⊥平面PAD;
(Ⅱ)取AD的中点E,连接PE,BE,易证平面PBE⊥平面ABCD,过M作MN⊥BE于点N,则MN⊥平面ABCD,由VM-ACD:VM-ABC=11:4可得:VM-ABCD:VM-ABC=15:4,进而可得MN的长,最后由在△PAE中,
=
得到答案.
(Ⅱ)取AD的中点E,连接PE,BE,易证平面PBE⊥平面ABCD,过M作MN⊥BE于点N,则MN⊥平面ABCD,由VM-ACD:VM-ABC=11:4可得:VM-ABCD:VM-ABC=15:4,进而可得MN的长,最后由在△PAE中,
| PM |
| MB |
| PE-MN |
| MN |
解答:
证明:(Ⅰ)在△ACD中,由AC=2AD=4,2DC=4
,
可得:AC2+AD2=CD2,
∴AC⊥AD,
∵平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,AC?底面ABCD,
∴AC⊥平面PAD,
又∵AC?平面MAC,
∴平面MAC⊥平面PAD;
解:(Ⅱ)取AD的中点E,连接PE,
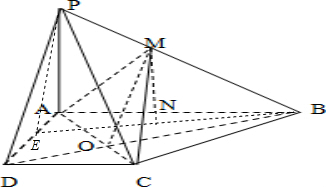
则PE⊥AD,则PE⊥平面ABCD,且PE=
,
连接BE,则平面PBE⊥平面ABCD,
过M作MN⊥BE于点N,则MN⊥平面ABCD,
∴S△ACD=
×AC×AD=
×2×4=4,
S△ABC=
×AC×AB•sin∠BAC=
×4
×4×
=8,
故Vp-ABCD=
(S△ACD+S△ABC)PE=
×(4+8)×
=4
,
VM-ABC=
S△ABC•MN=
MN,
由VM-ACD:VM-ABC=11:4得:VM-ABCD:VM-ABC=15:4,
即4
:
MN=15:4,
解得:MN=
在△PAE中,
=
=
| 5 |
可得:AC2+AD2=CD2,
∴AC⊥AD,
∵平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,AC?底面ABCD,
∴AC⊥平面PAD,
又∵AC?平面MAC,
∴平面MAC⊥平面PAD;
解:(Ⅱ)取AD的中点E,连接PE,

则PE⊥AD,则PE⊥平面ABCD,且PE=
| 3 |
连接BE,则平面PBE⊥平面ABCD,
过M作MN⊥BE于点N,则MN⊥平面ABCD,
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 | ||
2
|
故Vp-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
VM-ABC=
| 1 |
| 3 |
| 8 |
| 3 |
由VM-ACD:VM-ABC=11:4得:VM-ABCD:VM-ABC=15:4,
即4
| 3 |
| 8 |
| 3 |
解得:MN=
2
| ||
| 5 |
在△PAE中,
| PM |
| MB |
| PE-MN |
| MN |
| 3 |
| 2 |
点评:本题考查的知识点是平面与平面垂直的判定,棱锥的体积,熟练掌握空间线面关系的判定定理,性质定理及几何特征是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a,b∈{-1,0,1,2},则函数f(x)=ax2+2x+b有零点的概率为 A( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若实数x满足㏒2x=1+sinθ,则|x-4|+|x+1|=( )
| A、2x-3 | B、3-2x |
| C、-3 | D、5 |
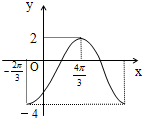 已知函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
 已知函数f(x)=sin(ωx-
已知函数f(x)=sin(ωx-