题目内容
已知函数f(x)=x3-x2-x+a的图象与x轴仅有一个交点,则a的取值范围为 .
考点:利用导数研究函数的极值
专题:计算题,导数的综合应用,不等式的解法及应用
分析:求出导数,求出单调区间,求出极值,曲线f(x)与x轴仅有一个交点,可转化成f(x)极大值<0或f(x)极小值>0即可.
解答:
解:函数f(x)=x3-x2-x+a的导数为f′(x)=3x2-2x-1,
当x>1或x<-
时,f′(x)>0,f(x)递增;
当-
<x<1时,f′(x)<0,f(x)递减.
即有f(1)为极小值,f(-
)为极大值.
∵f(x)在(-∞,-
)上单调递增,
∴当x→-∞时,f(x)→-∞;
又f(x)在(1,+∞)单调递增,当x→+∞时,f(x)→+∞,
∴当f(x)极大值<0或f(x)极小值>0时,曲线f(x)与x轴仅有一个交点.
即a+
<0或a-1>0,
∴a∈(-∞,-
)∪(1,+∞)
故答案为:(-∞,-
)∪(1,+∞).
当x>1或x<-
| 1 |
| 3 |
当-
| 1 |
| 3 |
即有f(1)为极小值,f(-
| 1 |
| 3 |
∵f(x)在(-∞,-
| 1 |
| 3 |
∴当x→-∞时,f(x)→-∞;
又f(x)在(1,+∞)单调递增,当x→+∞时,f(x)→+∞,
∴当f(x)极大值<0或f(x)极小值>0时,曲线f(x)与x轴仅有一个交点.
即a+
| 5 |
| 27 |
∴a∈(-∞,-
| 5 |
| 27 |
故答案为:(-∞,-
| 5 |
| 27 |
点评:本题主要考查了利用导数研究函数的极值,以及函数的单调性,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
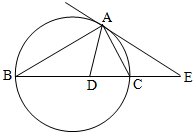 如图,△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.
如图,△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.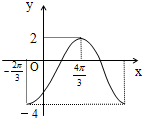 已知函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<