题目内容
已知点P(x,y)是圆(x+2)2+y2=1上任意一点.
(1)求P点到直线3x+4y+12=0的距离的最大值和最小值;
(2)求x-2y的最大值和最小值;
(2)求
的最大值和最小值.
(1)求P点到直线3x+4y+12=0的距离的最大值和最小值;
(2)求x-2y的最大值和最小值;
(2)求
| y-2 |
| x-1 |
考点:圆的标准方程
专题:直线与圆
分析:(1)求出圆心C(-2,0)到直线3x+4y+12=0的距离d=
,大于半径r=1,再根据P点到直线3x+4y+12=0的距离的最大值为d+r、最小值d-r,可得结论.
(2)令t=x-2y,则当圆(x+2)2+y2=1和此直线相切时,t取得最值.再根据圆心(-2,0)到直线x-2y-t=0的距离为1,求得t的值,即为所求.
(3)
表示圆上的点P(x,y)与点M(1,2)连线的斜率,设为k,则过点M的圆的切线方程为y-2=k(x-1),由圆心到切线的距离等于半径,求得k的值,可得
的最大值和最小值.
| 6 |
| 5 |
(2)令t=x-2y,则当圆(x+2)2+y2=1和此直线相切时,t取得最值.再根据圆心(-2,0)到直线x-2y-t=0的距离为1,求得t的值,即为所求.
(3)
| y-2 |
| x-1 |
| y-2 |
| x-1 |
解答:
解:(1)圆心C(-2,0)到直线3x+4y+12=0的距离d=
=
,大于半径r=1,
故P点到直线3x+4y+12=0的距离的最大值为d+r=
,最小值d-r=
.
(2)令t=x-2y,即y=
-
,表示斜率为
、在y轴上的截距为-
的直线,
故当此直线和圆(x+2)2+y2=1相切时,t取得最值.
由圆心(-2,0)到直线x-2y-t=0的距离为半径1,可得
=1,
求得t=-2-
,或t=-2+
,
故t=x-2y的最大值为-2+
,t=x-2y的最小值为-2-
.
(3)
表示圆上的点P(x,y)与点M(1,2)连线的斜率,
设为k,则过点M的圆的切线方程为y-2=k(x-1),
即 kx-y+2-k=0,由圆心到切线的距离等于半径,可得
=1,求得k=
,
故
的最大值为
,最小值为
.
| |-6+0+12| | ||
|
| 6 |
| 5 |
故P点到直线3x+4y+12=0的距离的最大值为d+r=
| 11 |
| 5 |
| 1 |
| 5 |
(2)令t=x-2y,即y=
| x |
| 2 |
| t |
| 2 |
| 1 |
| 2 |
| t |
| 2 |
故当此直线和圆(x+2)2+y2=1相切时,t取得最值.
由圆心(-2,0)到直线x-2y-t=0的距离为半径1,可得
| |-2-0-t| | ||
|
求得t=-2-
| 5 |
| 5 |
故t=x-2y的最大值为-2+
| 5 |
| 5 |
(3)
| y-2 |
| x-1 |
设为k,则过点M的圆的切线方程为y-2=k(x-1),
即 kx-y+2-k=0,由圆心到切线的距离等于半径,可得
| |-2k-0+2-k| | ||
|
3±
| ||
| 4 |
故
| y-2 |
| x-1 |
3+
| ||
| 4 |
3-
| ||
| 4 |
点评:本题主要考查直线的斜率公式,直线和圆相切的性质,点到直线的距离公式的应用,体现了转化的数学思想,属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
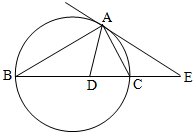 如图,△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.
如图,△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.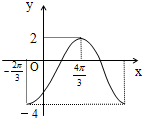 已知函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
 已知函数f(x)=sin(ωx-
已知函数f(x)=sin(ωx-