Question

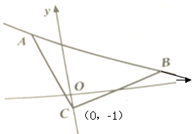如图，等腰直角△ABC的直角顶点C（0，-1），斜边AB所在的直线方程为x+2y-8=0．
（1）求△ABC的面积；
（2）求斜边AB中点D的坐标．

Answer 1

考点：中点坐标公式,直线的一般式方程与直线的垂直关系

专题：直线与圆

分析：（1）由点到直线距离公式求得C到AB边所在直线距离，然后由等腰直角三角形的性质求得AB的长度，代入三角形面积公式得答案；
（2）由等腰直角三角形斜边的高与斜边的中线重合，先求出斜边的高线所在直线方程，联立方程组求得斜边AB中点D的坐标．

解答： 解：（1）由点到直线的距离公式求得C到直线x+2y-8=0的距离为d=

|1×0+2×(-1)-8|

12+22

=2

5

．
根据等腰直角三角形斜边上的高等于斜边的2倍可得|AB|=4

5

．
则S△ABC=

1

2

×4

5

×2

5

=20；
（2）∵AB所在的直线方程为x+2y-8=0，斜率为-

1

2

，
则AB边上的高所在直线的斜率为2，高所在直线方程为y=2x-1，
联立

y=2x-1 x+2y-8=0

，解得

x=2 y=3

．
∴斜边AB中点D的坐标为（2，3）．

点评：本题考查了直线的一般式方程与直线垂直间的关系，考查了等腰直角三角形的性质，是基础题．