题目内容
设变量x、y满足
,则z=x+2y的最大值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:先画出满足条件的平面区域,求出A点的坐标,将z=x+2y变形为:y=-
x+
,得到函数过A(4,5)时,Z取到最大值.
| 1 |
| 2 |
| z |
| 2 |
解答:
解:画出满足条件的平面区域,
如图示:
 ,
,
联立方程
,解得:A(4,5),
将z=x+2y变形为:y=-
x+
,
显然函数y=-
x+
过A(4,5)时,
Z取到最大值,Z最大值=14.
故答案为:14.
如图示:
 ,
,联立方程
|
将z=x+2y变形为:y=-
| 1 |
| 2 |
| z |
| 2 |
显然函数y=-
| 1 |
| 2 |
| z |
| 2 |
Z取到最大值,Z最大值=14.
故答案为:14.
点评:本题考查了解得的线性规划问题,考查了数形结合思想,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知圆C:(x-1)2+(y-
)2=2与直线l:x+
y-6=0相交于A,B两点,O为坐标原点,则直线OA与直线OB的倾斜角之和为( )
| 3 |
| 3 |
| A、60° | B、90° |
| C、120° | D、150° |
已知点P是直线3x+4y+5=0上的动点,点Q为圆(x-2)2+(y-2)2=4上的动点,则|PQ|的最小值为( )
A、
| ||
| B、2 | ||
C、
| ||
D、
|
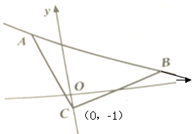 如图,等腰直角△ABC的直角顶点C(0,-1),斜边AB所在的直线方程为x+2y-8=0.
如图,等腰直角△ABC的直角顶点C(0,-1),斜边AB所在的直线方程为x+2y-8=0.