题目内容
设α∈(
,π),β∈(0,
),且tanβ=
,则( )
| π |
| 2 |
| π |
| 2 |
| 1-cosα |
| sinα |
| A、a-2β=0 | ||
| B、2α-3β=0 | ||
C、α+β=
| ||
D、α+β=
|
考点:三角函数的化简求值
专题:三角函数的求值
分析:根据三角函数的倍角公式进行化简即可.
解答:
解:tanβ=
=
=tan
,
∵α∈(
,π),∴
∈(
,
),
∴β=
,即a-2β=0,
故选:A
| 1-cosα |
| sinα |
1-1+2sin2
| ||||
2sin
|
| α |
| 2 |
∵α∈(
| π |
| 2 |
| α |
| 2 |
| π |
| 4 |
| π |
| 2 |
∴β=
| α |
| 2 |
故选:A
点评:本题主要考查三角函数的化简和求值,根据三角函数的倍角公式是解决本题的关键.

练习册系列答案
相关题目
设集合U=R,A={x∈N|x≤3},B={-2,-1,0,1,2},则(∁UA)∩B等于( )
| A、{-2,-1,0} |
| B、{-2,-1} |
| C、{1,2} |
| D、{0,1,2} |
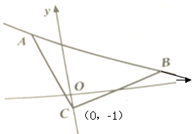 如图,等腰直角△ABC的直角顶点C(0,-1),斜边AB所在的直线方程为x+2y-8=0.
如图,等腰直角△ABC的直角顶点C(0,-1),斜边AB所在的直线方程为x+2y-8=0.