题目内容
已知函数f(x)=|x2-5x+4|,且方程f(x)=mx有三个不相等的实数根,则m= 且三个实根的和是 .
考点:函数的零点与方程根的关系
专题:计算题,作图题,函数的性质及应用
分析:方程f(x)=mx有三个不相等的实数根即函数f(x)=|x2-5x+4|与函数y=mx有三个不同的交点,从而作图确定根的位置,从而可得x2-5x+4=-mx仅有一个解;从而求出m,再代回求三根之和.
解答:
解:方程f(x)=mx有三个不相等的实数根即函数f(x)=|x2-5x+4|与函数y=mx有三个不同的交点,
作函数f(x)=|x2-5x+4|与函数y=mx的图象如下,
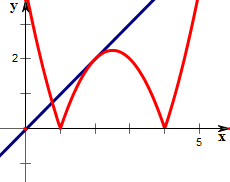
结合图象可知方程x2-5x+4=-mx仅有一个解;
故△=(m-5)2-16=0;
故m=1或m=9(舍去);
故m=1;
由x2-5x+4=x可化为x2-6x+4=0,
故x1+x2=6;
由由x2-5x+4=-x可化为x2-4x+4=0;
故x=2;
故三个实根的和是6+2=8;
故答案为:1,8.
作函数f(x)=|x2-5x+4|与函数y=mx的图象如下,

结合图象可知方程x2-5x+4=-mx仅有一个解;
故△=(m-5)2-16=0;
故m=1或m=9(舍去);
故m=1;
由x2-5x+4=x可化为x2-6x+4=0,
故x1+x2=6;
由由x2-5x+4=-x可化为x2-4x+4=0;
故x=2;
故三个实根的和是6+2=8;
故答案为:1,8.
点评:本题考查了零点的综合应用,同时考查了数形结合的数学思想的应用,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知点P是直线3x+4y+5=0上的动点,点Q为圆(x-2)2+(y-2)2=4上的动点,则|PQ|的最小值为( )
A、
| ||
| B、2 | ||
C、
| ||
D、
|
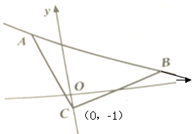 如图,等腰直角△ABC的直角顶点C(0,-1),斜边AB所在的直线方程为x+2y-8=0.
如图,等腰直角△ABC的直角顶点C(0,-1),斜边AB所在的直线方程为x+2y-8=0.