题目内容
已知a,b,c∈R,下列四个命题:
(1)若a>b 则ac2>bc2
(2)若
>
则a>b
(3)若a>b则a2>b2
(4)若a>b则
>
其中正确的个数是( )
(1)若a>b 则ac2>bc2
(2)若
| a |
| c |
| b |
| c |
(3)若a>b则a2>b2
(4)若a>b则
| 1 |
| b |
| 1 |
| a |
其中正确的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用,不等关系与不等式
专题:不等式的解法及应用
分析:(1)利用不等式的性质,可判断(1)正误;
(2)若c<0,可知a<b,从而知(2)正误;
(3)可举例说明(3)的正误;
(4)不妨令a=-1,b=-2,可对(4)作出正误判断.
(2)若c<0,可知a<b,从而知(2)正误;
(3)可举例说明(3)的正误;
(4)不妨令a=-1,b=-2,可对(4)作出正误判断.
解答:
解:(1)若a>b,当c=0时,ac2=bc2,故(1)错误;
(2)若
>
,则当c<0是,a<b,故(2)错误;
(3)若a>b,不妨令a=0,b=-2,则a2<b2,故(3)错误;
(4)若a>b,不妨令a=1,b=-2,则-
<1,故(4)错误;
综上所述,其中正确的个数是0个.
故选:A.
(2)若
| a |
| c |
| b |
| c |
(3)若a>b,不妨令a=0,b=-2,则a2<b2,故(3)错误;
(4)若a>b,不妨令a=1,b=-2,则-
| 1 |
| 2 |
综上所述,其中正确的个数是0个.
故选:A.
点评:本题考查命题的真假判断与应用,着重考查不等式的性质的应用,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
数列{an}的通项公式为an=2n+4n-2,则数列{an}的前n项和sn=( )
| A、2n+2n2-1 |
| B、2n+2n2-2 |
| C、2n+1+2n2-1 |
| D、2n+1+2n2-2 |
设x、y满足约束条件
,若x2+y2≥a恒成立,则实数a的最大值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知三条不重合的直线m,n,l和两个不重合的平面α、β,下列命题中正确命题个数为( )
①若m∥n,n?α,则m∥α;②若l⊥α,m⊥β且l⊥m则α⊥β
③若l⊥n,m⊥n,则l∥m④若α⊥β,α∩β=m,n?β,n⊥m,则n⊥α
①若m∥n,n?α,则m∥α;②若l⊥α,m⊥β且l⊥m则α⊥β
③若l⊥n,m⊥n,则l∥m④若α⊥β,α∩β=m,n?β,n⊥m,则n⊥α
| A、1 | B、2 | C、3 | D、4 |
 学校为了调查学生在课外读物方面的支出情况,将支出分区间[20,30)、[30,40)、[40,50)、[50,60)进行统计,现抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有24人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,将支出分区间[20,30)、[30,40)、[40,50)、[50,60)进行统计,现抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有24人,则n的值为( )| A、80 | B、800 |
| C、72 | D、720 |
过双曲线
-
=1(a>0,b>0)的一个焦点作实轴的垂线,交双曲线于A,B两点,若线段AB的长度恰等于焦距,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知变量x,y满足约束条件
,则z=4x+y的最小值为( )
|
| A、55 | B、-55 | C、5 | D、-5 |
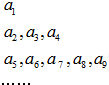 将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.
将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.