题目内容
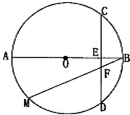如图，AB为半径为2的圆O的直径，CD为垂直于AB的一条弦，垂足为E，弦BM与CD交于点F．则AC2+BF•BM=考点：与圆有关的比例线段
专题：直线与圆
分析：连结AM、AC、BC，由题设条件推导出A、M、F、E四点共圆，△ACB∽△AEC，从而得到AC2+BF•BM=4BE+4AE，由此能求出结果．
解答：
解：连结AM、AC、BC，
∵AB为半径为2的圆O的直径，∴AM⊥BM，AC⊥BC，
∵CD为垂直于AB的一条弦，垂足为E，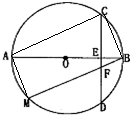
弦BM与CD交于点F．
∴∠AMF+∠AEF=180°，
∴A、M、F、E四点共圆，
∴BF•BM=BE•BA=4BE，
∵AC⊥BC，CE⊥AB，
∴△ACB∽△AEC，∴
=
，
∴AC2=AE•AB=4AE，
∴AC2+BF•BM=4BE+4AE=4AB=16．
故答案为：16．
∵AB为半径为2的圆O的直径，∴AM⊥BM，AC⊥BC，
∵CD为垂直于AB的一条弦，垂足为E，
弦BM与CD交于点F．∴∠AMF+∠AEF=180°，
∴A、M、F、E四点共圆，
∴BF•BM=BE•BA=4BE，
∵AC⊥BC，CE⊥AB，
∴△ACB∽△AEC，∴
| AC |
| AE |
| AB |
| AC |
∴AC2=AE•AB=4AE，
∴AC2+BF•BM=4BE+4AE=4AB=16．
故答案为：16．
点评：本题考查与圆有关的比例线段的求法，是中档题，解题时要注意数形结合思想的合理运用，注意切割线定理的合理运用．
练习册系列答案
相关题目
学校为了调查学生在课外读物方面的支出情况，将支出分区间[20，30）、[30，40）、[40，50）、[50，60）进行统计，现抽出了一个容量为n的样本，其频率分布直方图如图所示，其中支出在[50，60）元的同学有24人，则n的值为（ ）