题目内容
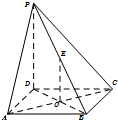 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,AC与BD交于点O,E为PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,AC与BD交于点O,E为PB的中点.(Ⅰ)求证:EO∥平面PAD;
(Ⅱ)求证:AC⊥PB.
考点:直线与平面垂直的性质,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)通过三角形中位线的性质可得OE∥PD,进而根据线面平行的判定定理可以证明出EO∥平面PAD;
(2)先分别证明出AC⊥BD,PD⊥AC,进而根据线面垂直的判定定理证明出AC⊥平面PBD,即可得出结论.
(2)先分别证明出AC⊥BD,PD⊥AC,进而根据线面垂直的判定定理证明出AC⊥平面PBD,即可得出结论.
解答:
证明:(1)因为 底面ABCD是正方形,AC与BD交于点O,
所以 O为BD的中点.
又 E为PB的中点,
所以 EO∥PD.
因为 EO?平面PAD,PD?平面PAD,
所以 EO∥平面PAD.
(2)∵底面ABCD是正方形,∴AC⊥BD,
∵PD⊥底面ABCD,AC?平面ABCD,
∴PD⊥AC,
又 PD∩BD=D,
所以 AC⊥平面PBD.
所以 AC⊥⊥PB.
所以 O为BD的中点.
又 E为PB的中点,
所以 EO∥PD.
因为 EO?平面PAD,PD?平面PAD,
所以 EO∥平面PAD.
(2)∵底面ABCD是正方形,∴AC⊥BD,
∵PD⊥底面ABCD,AC?平面ABCD,
∴PD⊥AC,
又 PD∩BD=D,
所以 AC⊥平面PBD.
所以 AC⊥⊥PB.
点评:本题主要考查了线面平行,线面垂直的判定定理的应用.考查了学生对线面平行,线面垂直判定定理的记忆.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合A={x|x2-2x-3<0},B={y|1≤y≤4},则下列结论正确的是( )
| A、A∩B=∅ |
| B、(∁UA)∪B=(-1,+∞) |
| C、A∩B=(1,4] |
| D、(∁UA)∩B=[3,4] |
若关于x的方程25-|x+1|-4×5-|x+1|=m有实根,则实数m的取值范围是( )
| A、m<0 | B、m≥-4 |
| C、-4≤m<0 | D、-3≤m<0 |